Линейная функция
Содержание:
Пример решения
Существует некоторый тип задач, в которых нужно исследовать и построить график функции y = k/x. Разобрать решение можно на примере y = 5 / (x – 3). Следует воспользоваться алгоритмом:

- D(5 / (x – 3)) = (-inf;3) U (3;+inf).
- Нули функции. По ОУ: y = 5 / (0 – 3) = – 5/3. По ОХ: 5 / (x – 3) = 0. Если решить уравнения, то у него нет корней.
- Знаковые промежутки: (-inf;3) и (3;+inf).
- Непериодическая.
- Четность: 5 / (-x – 3) = – 5 / (x + 3). Нечетная: – 5 / (x + 3) не равно 5 / (x – 3).
- Экстремумы: y’ = [5 / (x – 3)] = – 5 / (x – 3)^2 = 0. Уравнение не имеет решений, а это значит, что максимума и минимума нет.
- Не является монотонной.
Чтобы построить график функции y = k / x + 3 (к = 5), нужно составить таблицу для его построения.
| х | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | |
| у | -5/7 | -5/6 | -1 | -1,2 | -5/3 | -2,5 | -5 | нет | 5 |
Таблица 1. Зависимость значения функции от ее аргумента.
После составления таблицы нужно начертить ДСК. На ней следует отмечать точки, а затем их плавно соединить (рис. 2).
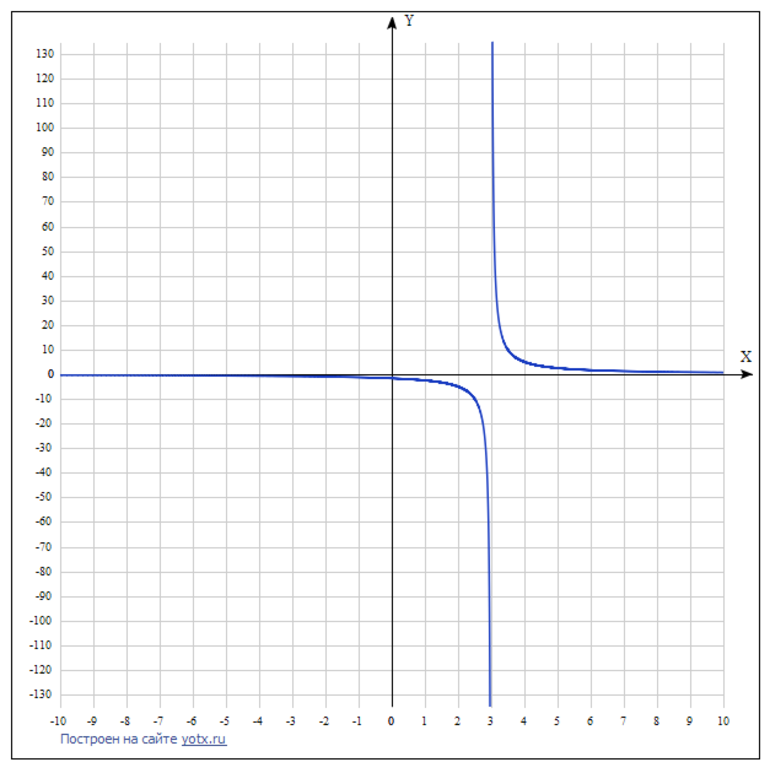
Рисунок 2. График обратной пропорциональности y = k / x – 3 при к = 5.
Таким образом, графиком обратной пропорциональности является гипербола, а прямой пропорциональности — прямая. Поведение функции исследуется по специальному алгоритму, который позволяет легко построить ее график и выяснить некоторые свойства.
Предыдущая
АлгебраРешение матриц методы решений и примеров для чайников, формулы вычислений и действий с матрицами
Следующая
АлгебраВозведение дроби в степень правило, как возвести алгебраическую дробь в степень, калькулятор примеров, свойства дробных степеней, как решать примеры со степенью
Абстрактная алгебра
Термин «линейная функция», или, точнее, «линейная однородная функция», часто применяется для линейного отображения векторного пространства X{\displaystyle X} над некоторым полем k{\displaystyle k} в это поле, то есть для такого отображения fX→k{\displaystyle f:X\to k}, что для любых элементов x,y∈X{\displaystyle x,y\in X} и любых α,β∈k{\displaystyle \alpha ,\beta \in k} справедливо равенство
- f(αx+βy)=αf(x)+βf(y){\displaystyle f(\alpha x+\beta y)=\alpha f(x)+\beta f(y)}
причём в этом случае вместо термина «линейная функция» используются также термины линейный функционал и линейная форма — также означающие линейную однородную функцию определённого класса.
Как решать задачи на линейную функцию «y = kx + b»
Рассмотрим задачу.
Построить график функции «». Найти по графику:
- значение «» соответствующее значению «» равному ;
- значение «», если значение «» равно
.
Вначале построим график функции «».
Используем правила, по которым мы выше.
Для построения графика функции «» достаточно найти всего две точки.
Выберем два произвольных числовых значения для «». Для удобства расчетов выберем числа
«» и «».
Выполним расчеты и запишем их результаты в таблицу.
| Точка | Координата по оси «» | Координата по оси «» |
|---|
Отметим полученные точки на прямоугольной системе координат.
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«».
Теперь работаем с построенным графиком функции «».
Требуется найти значение «»,
соответствующее значению «», которое равно .
Тему
«» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».
В этому уроке для решения задачи выше вспомним только основные моменты.
Запомните!
Чтобы найти значение «» по известному значению «» на графике
функции необходимо:
- провести перпендикуляр от оси «»
()
из заданного числового значения «»
до пересечения
с графиком функции; - из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси
«»
(); - полученное числовое значение на оси «» и будет искомым значением.
По правилам выше найдем на построенном ранее графике функции «»
необходимые значения функции «» для
«» равным .
Запишем полученные результаты в таблицу.
| Заданное значение «» | Полученное с графика значение «» |
|---|
Переходим ко второму заданию задачи. Требуется найти значение «»,
если значение «» равно .
Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси
«».
Запишем полученные результаты в таблицу.
| Заданное значение «» | Полученное с графика значение «» |
|---|
Как проверить, проходит ли график через точку
Рассмотрим другое задание.
Запомните!
Чтобы проверить принадлежность точки графику функции нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси
«» вместо
«», а координату по оси
«» вместо «») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка
не принадлежит графику функции.
(верно)
проходит
(неверно)
не проходит
Как найти точки пересечения графика с осями
Рассмотрим задачу.
Найти координаты точек пересечения графика функции «» с осями координат.
Для начала построим график функции «» и на графике отметим точки пересечения
с осями.
найдем координаты двух точек функции
«».
Выберем два произвольных числовых значения для «» и рассчитаем значение
«» по формуле
функции. Например, для и
.
| Точка | Координата по оси «» | Координата по оси «» |
|---|
Отметим полученные точки на системе координат и проведем через них прямую.
Тем самым мы построим график функции «».
Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.
Запомните!
Чтобы найти координаты точки пересечения графика функции с осью
«»
()
нужно:
- приравнять координату точки по оси
«» к нулю
; - подставить вместо «» в формулу функции ноль и найти значение
«»; - записать полученные координаты точки пересечения с осью
«».
Подставим вместо «» в формулу функции «» число ноль.
Запомните!
Чтобы найти координаты точки пересечения графика функции с осью
«»
()
нужно:
- приравнять координату точки по оси
«» к нулю
; - подставить вместо «» в формулу функции ноль и найти значение
«»; - записать полученные координаты точки пересечения с осью
«».
Подставим вместо «» в формулу функции «» число ноль.
Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните
«правило противоположности».
Важно!
Если нужно найти координаты точки пересечения графика с осью
«», то приравниваем
«» к нулю.
И наооборот. Если нужно найти координаты точки пересечениа графика с осью
«»,
то приравниваем «» к нулю.
Нелинейные функции
Для функций, не являющихся линейными, употребляют термин нелинейные функции.
То же относится и к употреблению слова нелинейные в отношении других объектов, не обладающих свойством линейности, например — нелинейные дифференциальные уравнения.
Обычно термин используется, когда функциональную зависимость вначале приближают линейной, а потом переходят к изучению более общего случая, часто начиная с младших степеней, например рассматривая квадратичные поправки.
Нелинейные уравнения достаточно произвольны. К примеру, нелинейной является функция y=x2{\displaystyle y=x^{2}}.
В ряде случаев этот термин может применяться и к зависимостям f=kx+b{\displaystyle f=kx+b}, где b≠{\displaystyle b\neq 0}, то есть к неоднородным линейным функциям, поскольку они не обладают свойством линейности, а именно в этом случае f(x1+x2)≠f(x1)+f(x2){\displaystyle f(x_{1}+x_{2})\neq f(x_{1})+f(x_{2})} и f(cx)≠cf(x){\displaystyle f(cx)\neq cf(x)}.
Например, нелинейной зависимостью считают σ(τ){\displaystyle \sigma (\tau )} для материала с упрочнением (см. теория пластичности).
Свойства
- k{\displaystyle k} (угловой коэффициент прямой) является тангенсом угла α (α∈;π2)∪(π2;π)),{\displaystyle \alpha ~(\alpha \in [0;{\frac {\pi }{2}})\cup ({\frac {\pi }{2}};\pi )),} который прямая образует с положительным направлением оси абсцисс.
- При k>{\displaystyle k>0}, прямая образует острый угол с положительным направлением оси абсцисс.
- При k<{\displaystyle k<0}, прямая образует тупой угол с положительным направлением оси абсцисс.
- При k={\displaystyle k=0}, прямая параллельна оси абсцисс.
Угол между двумя прямыми, задаваемыми уравнениями
y=k1x+b1,{\displaystyle y=k_{1}x+b_{1},} и y=k2x+b2,{\displaystyle y=k_{2}x+b_{2},} определяется равенством:
tgα=|k1−k21+k1k2|,{\displaystyle \mathrm {tg} \,\alpha =\left|{\frac {k_{1}-k_{2}}{1+k_{1}k_{2}}}\right|,}
где k1k2≠−1,{\displaystyle k_{1}k_{2}\neq -1,} то есть прямые не являются взаимно перпендикулярными; при k1=k2, α={\displaystyle k_{1}=k_{2},~\alpha =0} и прямые параллельны.
- b{\displaystyle b} является показателем ординаты точки пересечения прямой с осью ординат.
- При b={\displaystyle b=0}, прямая проходит через начало координат.
Общие сведения
Функцией называется некоторая зависимость переменных друг от друга. В некоторых случаях неизвестные величины могут быть выражены системой конкретных значений, интервалами, а также другими функциональными выражениями. Последний класс называется сложным или составным. Различают зависимые и независимые переменные (аргументы). Второй тип может принимать любые значения, кроме тех, которые превращают выражение в неопределенность.
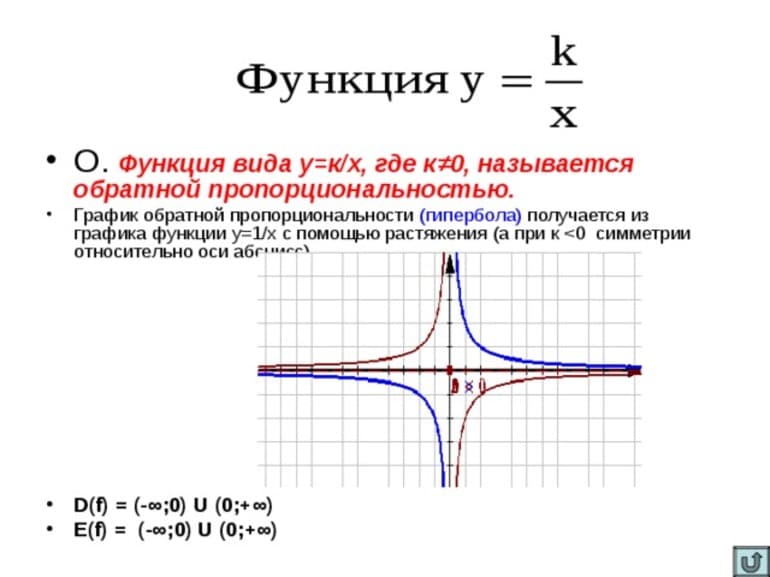
Однако аргументы необходимо также обследовать, поскольку они могут обратить тождество в пустое множество. Одним из таких примеров является функция у = к / х. Ее аргумент x может принимать любые значения, кроме 0. Именно это число превращает уравнение в неопределенность, поскольку в математике существует следующее правило: запрещается делить на 0.
Следует отметить, что существует функция y = k/x и ее график — кривая, имеющая название гипербола. Многие путают его с параболой (в степени 2). Однако она является квадратичной. График строится в системе координат, которая называется декартовой. Кроме того, в математике встречается еще одно уравнение вида y = кх. Ее графиком является прямая.
Прямоугольная система координат
В математике существуют специальные инструменты для построения графиков функций. Одним из них считается распространенная прямоугольная система координат. Она может быть на плоскости и в пространстве. Поскольку y = k/x и y = kx являются элементарными, то для иллюстрации их графиков используется однородная прямоугольная декартовая система координат (рис. 1), элементом которой является точка.
Для декартовой системы на плоскости имеется только две координаты: по взаимно перпендикулярным осям ординат (ОУ) и абсцисс (ОХ). Они пересекаются в некоторой точке О, которая называется началом координат.
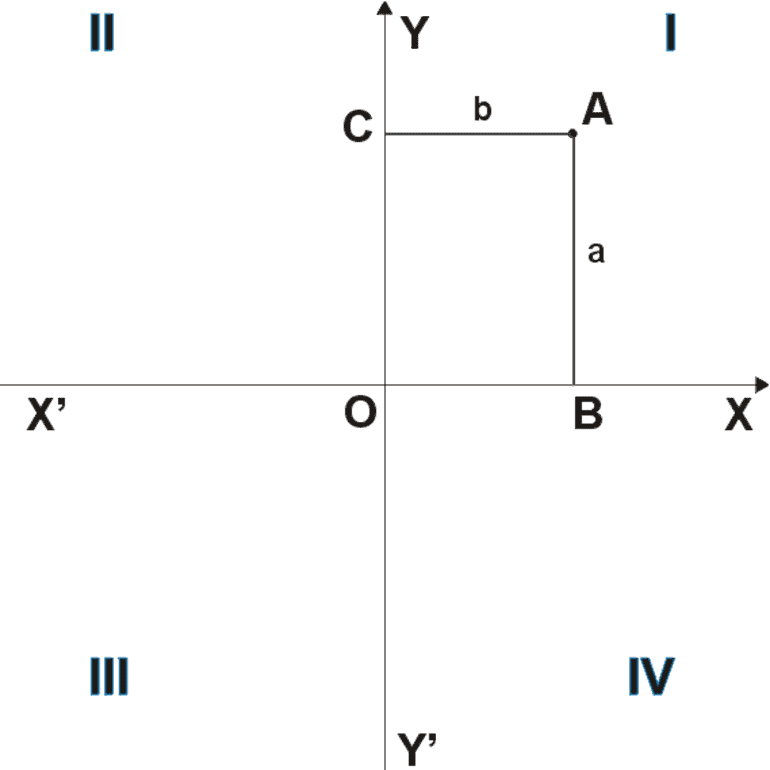
Рисунок 1. Прямоугольная декартова система координат (ДСК).
При указании координат нужно учитывать четверть. От нее зависит знак. Оси ординат (игрек) и абсцисс (икс) делят систему на четыре четверти. Они обозначаются римскими цифрами (рис. 1) и имеют такие свойства:
- Первая — I: координаты x и y являются положительными числами, т. е. x > 0 и y > 0.
- II: x < 0 и y > 0.
- III: x < 0 и y < 0.
- IV: x > 0 и y < 0.
Базовыми знаниями являются правильное нахождение координат произвольной точки и их запись. Например, на рисунке 1 нужно найти координаты С. Их нужно искать по следующему алгоритму:
- Опустить из точки перпендикуляры на ОУ и ОХ: b и a соответственно.
- Найти координаты по х и у (размерность шкалы деления осей нужно задавать при построении ДСК): B и С соответственно.
- Записать значения: C(В;С).
Допускается задавать одну шкалу в одних единицах, а вторую — в других. Например, при построении графика y = 100x можно задавать х в виде единичных значений, а вот уже у будут исчисляться сотнями. Чтобы приступать к дальнейшему изучению материала, математики рекомендуют потренироваться в нахождении координат любых точек.
Коэффициент пропорциональности

В математических дисциплинах бывает два типа пропорциональности — прямая и обратная. Они применяются для описания различных процессов, исследования дифференциальных уравнений, физических величин и законов.
Прямой пропорциональностью называется некоторая линейная функция вида y = kx, в которой аргументом является х, а к — коэффициент прямой пропорциональности. Иными словами, произведение к на аргумент x есть величина, определяющая прямую пропорциональную зависимость одной величины от другой. Обратной пропорциональностью называется некоторая функция вида y = k/x, значение аргумента которой никогда не равно нулю.
Графиком линейной функции вида y = kx является прямая, проходящая через начало координат в точке О(0;0). От к зависит угол наклона прямой. Если к > 0, то он является острым, т. е. его значение меньше 90 градусов. При к < 0 угол наклона больше 90 градусов (тупой).
Для обратной пропорциональности, заданной уравнением у = к / х, значение коэффициента влияет на расположение гиперболы в четвертях ДСК. Если к > 0, то она располагается в I и III. Когда к < 0, тогда ее расположение заключено во II и IV четвертях.
Как по графику определить коэффициент k?
- Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента \(k\) плюс, если убывает – минус.
- Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:

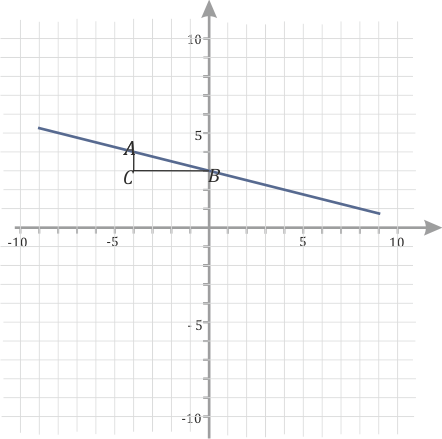
Чтобы определить значение \(k\) по модулю (то есть, без учета знака), надо вертикальную сторону треугольника поделить на горизонтальную. Можно использовать правило для запоминания: «стоячий бьет лежачего». В данных случаях \(|k|=\frac{AC}{BC}\). То есть на первом графике \(k=2\),а на втором \(k=-\frac{1}{4}\).
Как по графику функции определить значение \(b\)?
Очень просто — прямая пересекает ось \(y\) всегда в точке \(b\). Вы можете это увидеть на предыдущем графике.
Пример (ОГЭ): На рисунке изображены графики функций вида \(y=kx+b\). Установите соответствие между графиками функций и знаками коэффициентов \(k\) и \(b\).
A. 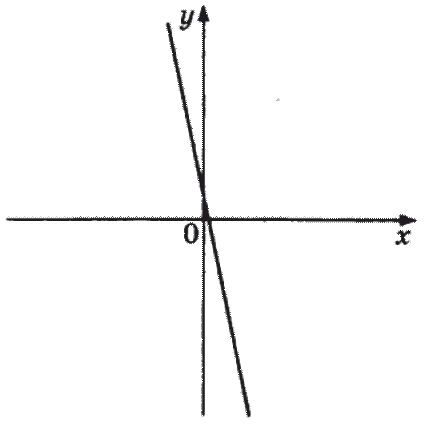 B.
B.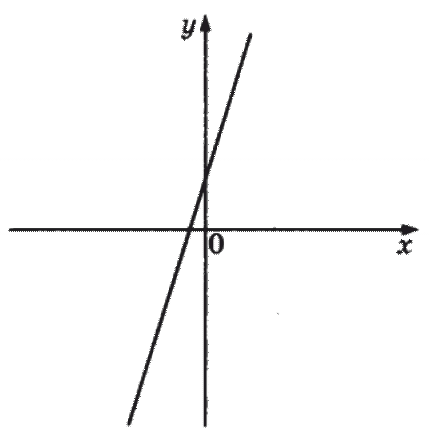 C.
C.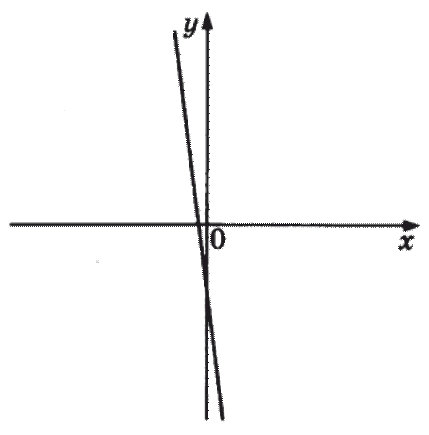
Коэффициенты
| 1) \(k>0\),\(b>0\) | 2) \(k<0\), \(b>0\) | 3) \(k<0\), \(b<0\) | 4) \(k>0\), \(b<0\) |
Решение:
А. – функция убывает, поэтому \(k<0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 2).
B. — функция возрастает — \(k>0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 1).
C. – функция убывает — \(k<0\). Точка пересечения оси \(y\) и прямой находится ниже нуля, значит \(b<0\). Подходит вариант под цифрой 3).Ответ: 213.