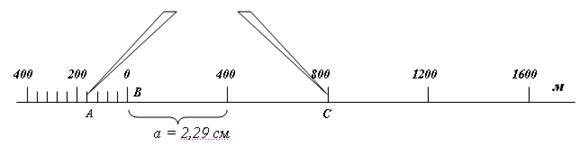
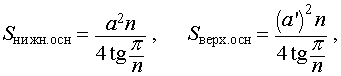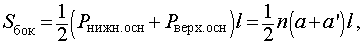Геометрические фигуры. прямоугольная пирамида

Стандартные задания на пирамиды (Sосн,Sбок ,ha)

Известны стороны основания – а и высота пирамиды – h. Необходимо найти:

1. Sосн

2. Sбок  ,ha

3. ∠(AB)

4. ∠(SC)

Решение:

1. Найти Sосн

Если есть ∆АВС (рис. 3), сторона которого равна а, то

Рис. 3

2. Найти Sбок ,hа

Отрезок SC1 называется апофемой ha(рис. 2). Апофему найдем из прямоугольного треугольника SC1O. Известен катет SO=h, второй катет С1О найдем из ∆АВС (рис. 3).

Для начала найдем высоту АА1 из прямоугольного треугольника АА1С:

Высота АА1 состоит из радиуса вписанной окружности r=С1О и из радиуса описанной окружности R (причем R=2r). 

Следовательно

Зная катеты ∆SC1O, мы можем найти гипотенузу

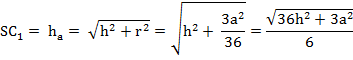
Найдя апофему haможно без труда найти

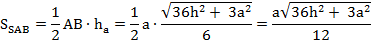
И

Из чего состоит фигура?

Познакомившись с определением пирамиды (пирамида в геометрии является полиэдром), можно переходить к рассмотрению элементов, которыми она образована. Приведем еще раз пример пирамиды.

На данном рисунке изображена шестиугольная пирамида. Так она называется по причине того, что в основании фигуры расположен шестиугольник. Взглянув на рисунок, можно выделить три основных геометрических элемента, которые составляют пирамиду:

• вершины;
• ребра;
• грани.

Начнем характеристику фигуры с вершин. Они являются «острыми» концами пирамиды. Всего у фигуры n+1 вершина, что становится очевидным, если вспомнить об n вершинах основания и одной точке H, не принадлежащей основанию. Точка H является особенной вершиной фигуры, поскольку она участвует в определении различных типов пирамид. Вершина H отличается от остальных вершин тем, что в ней пересекаются все n треугольников фигуры.

Ребра — это отрезки, соединяющие между собой вершины в единую конструкцию. Ребра пирамиды бывают двух типов: во-первых, это ребра основания, количество которых равно n, во-вторых, это ребра боковой поверхности, их число также равно n. Таким образом, число ребер рассматриваемой фигуры равно 2*n.

Грани, или стороны — важные элементы любой пирамиды, которые придают фигуре объемный вид. Грани у фигуры, как и ребра, бывают двух типов: во-первых, это основание пирамиды, которое представляет собой плоский многоугольник с n вершинами и n сторонами, во-вторых, это треугольники боковой поверхности. Количество треугольников любой пирамиды равно n. В итоге рассматриваемый полиэдр состоит из n+1 одной грани.

В середине XVIII века ученый из Швейцарии Леонард Эйлер опубликовал в одном из своих трудов теорему, которая связывает количества рассмотренных элементов полиэдра в единое равенство. Теорема гласит: если взять сумму граней и вершин, а затем из нее вычесть число 2, то получается сумма всех ребер полиэдра. Для пирамиды с n-угольным основанием имеем:

Что собой представляет пирамида?

С точки зрения стереометрии (геометрия трехмерного пространства), можно дать следующее определение пирамиды: пирамидой называется трехмерная фигура, которая ограничена треугольными гранями и одной многоугольной гранью. Данное определение является весьма простым и геометрически правильным. Тем не менее оно не позволяет ясно представить себе, о какой фигуре идет речь.

Можно дать более ясное определение пирамиды: пирамида — это фигура, которая получается в результате соединения прямыми отрезками некоторой точки в пространстве с вершинами выбранного многоугольника. Предположим, что у нас имеется n-угольник (n — целое число), расположенный в некоторой плоскости. Выберем произвольную точку пространства, которая не лежит в плоскости n-угольника. Для определенности назовем эту точку буквой H. Если отрезками соединить все вершины n-угольника с точкой H, то мы получим пирамидальную поверхность. Если к ней добавить еще n-угольное основание, то образованная фигура будет пирамидой.

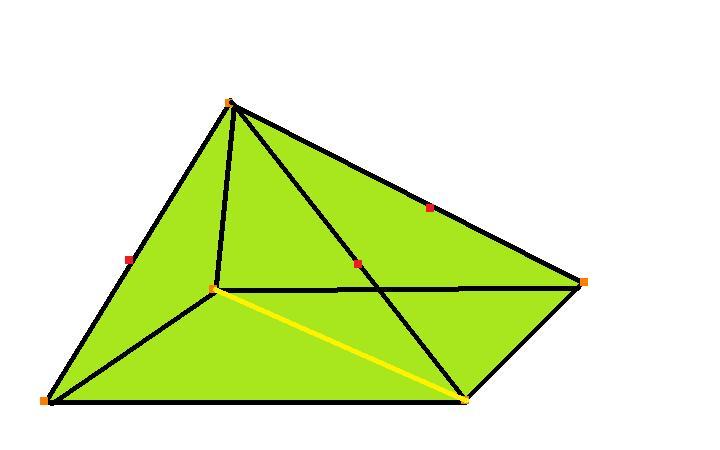
Выше схематический рисунок демонстрирует четырехугольную пирамиду произвольного типа, построенную по описанному выше способу.

Пирамиды и их апофемы

Для начала дадим определение пирамиде с точки зрения геометрии. Эта фигура представляет собой объемное тело, образованное одним n-угольником (основание) и n треугольниками (боковые стороны). Последние соединены в одной точке, которая называется вершиной. Расстояние от нее до основания — это высота фигуры. Если она попадает на геометрический центр n-угольника, то пирамида называется прямой. Если к тому же n-угольник имеет равные углы и стороны, то фигура называется правильной. Ниже показан пример пирамиды.

Что такое апофема для такой фигуры? Это перпендикуляр, который соединяет стороны n-угольника с вершиной фигуры. Очевидно, что она представляет собой высоту треугольника, являющегося боковой стороной пирамиды.

Апофему удобно использовать при решении геометрических задач с правильными пирамидами. Дело в том, что для них все боковые грани являются равными друг другу равнобедренными треугольниками. Последний факт означает, что все n апофем равны, поэтому для правильной пирамиды можно говорить об одной-единственной такой прямой.

Свойства апофемы

Их мало, но все же их нужно помнить. В целом это следствия, вытекающие из определения. Итак, апофема в правильной пирамиде:

1. Опущена на сторону основания под углом 90 градусов.
2. Делит сторону, на которую опущена, пополам, так как является высотой в равнобедренном/равностороннем треугольнике и по совместительству — медианой.

В правильной пирамиде все апофемы равны, так как все ее боковые грани также одинаковые. При нахождении длины апофемы вам придется воспользоваться как свойствами многоугольника, так и свойствами многогранника. Как же найти числовое значение апофемы в правильной пирамиде?

Решение задачи 1

Стороны основания правильной усеченной четырехугольной пирамиды  равны 3 см и 9 см, высота – 4 см. Найти площадь боковой поверхности.

Рис. 5. Иллюстрация к задаче 1

Решение. Проиллюстрируем условие:

Задано: , , 

Через точку О проведем прямую MN параллельно двум сторонам нижнего основания, аналогично через точку  проведем прямую  (рис. 6). Поскольку в основаниях усеченной пирамиды квадраты и построения параллельны, получим трапецию, равную боковым граням. Причем ее боковая сторона будет проходить через середины верхнего и нижнего ребра боковых граней и являться апофемой усеченной пирамиды.

Рис. 6. Дополнительные построения

Рассмотрим полученную трапецию  (рис. 6). В этой трапеции известно верхнее основание, нижнее основание и высота. Требуется найти боковую сторону, которая является апофемой заданной усеченной пирамиды. Проведем  перпендикулярно MN. Из точки  опустим перпендикуляр NQ. Получим, что большее основание разбивается на отрезки по три сантиметра (). Рассмотрим прямоугольный треугольник , катеты в нем известны, это египетский треугольник, по теореме Пифагора определяем длину гипотенузы: 5 см.

Теперь есть все элементы для определения площади боковой поверхности пирамиды:

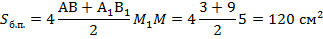
Как найти апофему пирамиды

Ее можно найти, применяя все ранее полученные знания, вот всего лишь несколько примеров:

• Если известны боковое ребро и сторона основания. Так как апофема делит сторону основания пополам и образует с ней угол в 90 градусов, то найти ее из прямоугольного треугольника по теореме Пифагора вам не составит труда. Также можно найти апофему, используя знания соотношений в прямоугольном треугольнике.
• Если известен радиус вписанной окружности в основание правильной пирамиды и высота всей фигуры. Радиус, проведенный к точке касания, перпендикулярен касательной, и апофема перпендикулярна этой стороне основания (которая является касательной к вписанной окружности). Высота фигуры перпендикулярна основанию и попадает в центр окружности, вписанной в основание пирамиды. Следовательно, радиус и высота фигуры являются катетами и образуют прямой угол, а вместе с апофемой — прямоугольный треугольник. И опять же по теореме Пифагора или через соотношения в прямоугольном треугольнике вы легко найдете апофему.

Также если дана площадь грани и известно основание.

В любом случае при нахождении апофемы вам придется вспоминать все основные законы и правила планиметрии. Если неизвестны какие-то элементы из этого списка, то вы можете оперировать данными параметрами, и, постепенно находя вышеописанные данные, найти апофему вам не составит труда. Надеемся, что наша статья помогла вам в освоении такой интересной темы.

Теоремы, связывающие пирамиду с другими геометрическими телами

Описание сферы вокруг правильной пирамиды:SD — высота пирамиды.AD — радиус окружности, описывающей основание.В — середина ребра боковой граниС — точка пересечения плоскостей проходящих через середину рёбер перпендикулярно им.AC=CS — радиус сферы описывающей пирамиду

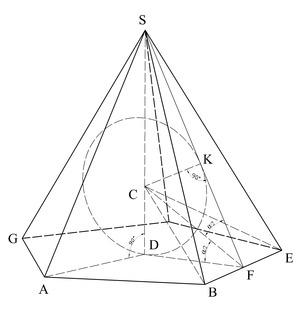Сфера, вписанная в правильную пирамиду:D — центр основанияSF — апофемаASD — биссекторная плоскость угла между боковыми гранямиBCE — биссекторная плоскость угла между основанием и боковой граньюС — точка пересечения всех биссекторных плоскостейCK=CD — радиус сферы вписанной в пирамиду

Сфера

• около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им. Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу;
• в пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.

Конус

• Конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие);
• Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые рёбра пирамиды равны между собой (необходимое и достаточное условие);
• Высоты у таких конусов и пирамид равны между собой.

Цилиндр

• Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.
• Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания пирамиды. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды — вписанный многоугольник (необходимое и достаточное условие).

Решение задачи 2

Пирамида пересечена плоскостью, параллельной основанию. Докажите на примере треугольной пирамиды, что боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части.

Доказательство. Проиллюстрируем:

Рис. 7. Иллюстрация к задаче 2

Задана пирамида РАВС. РО – высота пирамиды. Пирамида рассечена плоскостью , получена усеченная пирамида , причем . Точка  – точка пересечения высоты РО с плоскостью основания усеченной пирамиды . Необходимо доказать:

Ключом к решению является свойство параллельных плоскостей. Две параллельные плоскости рассекают любую третью плоскость так, что линии пересечения параллельны. Отсюда: . Из параллельности соответствующих прямых вытекает наличие четырех пар подобных треугольников:

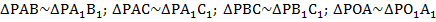
Из подобия треугольников вытекает пропорциональность соответствующих сторон. Важная особенность заключается в том, что коэффициенты подобия у этих треугольников одинаковы:

Отсюда:

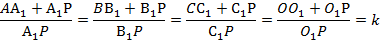
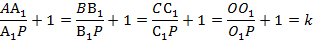
Что и требовалось доказать.

Свойства пирамиды.

     1. Когда все боковые ребра имеют одинаковую величину, тогда:

• около основания пирамиды легко описать окружность, при этом вершина пирамиды будет проецироваться в центр этой окружности;
• боковые ребра образуют с плоскостью основания одинаковые углы;
• кроме того, верно и обратное, т.е. когда боковые ребра образуют с плоскостью основания равные углы, либо когда около основания пирамиды можно описать окружность и вершина пирамиды будет проецироваться в центр этой окружности, значит, все боковые ребра пирамиды имеют одинаковую величину.

     2. Когда боковые грани имеют угол наклона к плоскости основания одной величины, тогда:

• около основания пирамиды легко описать окружность, при этом вершина пирамиды будет проецироваться в центр этой окружности;
• высоты боковых граней имеют равную длину;
• площадь боковой поверхности равняется ½ произведения периметра основания на высоту боковой грани.

     3. Около пирамиды можно описать сферу в том случае, если в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы станет точка пересечения плоскостей, которые проходят через середины ребер пирамиды перпендикулярно им. Из этой теоремы делаем вывод, что как около всякой треугольной, так и около всякой правильной пирамиды можно описать сферу.

     4. В пирамиду можно вписать сферу в том случае, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в 1-ной точке (необходимое и достаточное условие). Эта точка станет центром сферы.

     5. Конус будет вписанным в пирамиду, когда вершины их совпадут, а основание конуса будет вписанным в основание пирамиды. При этом вписать конус в пирамиду можно лишь в том случае, если апофемы пирамиды имеют равные величины (необходимое и достаточное условие).

     6. Конус будет описанным около пирамиды, если их вершины совпадут, а основание конуса будет описано около основания пирамиды. При этом описать конус около пирамиды можно лишь в том случае, если все боковые ребра пирамиды имеют одинаковые величины (необходимое и достаточное условие). Высоты у этих конусов и пирамид одинаковы.

     7. Цилиндр будет вписанным в пирамиду, если 1-но его основание совпадет с окружностью, которая вписана в сечение пирамиды плоскостью, параллельной основанию, а второе основание будет принадлежать основанию пирамиды.

     8. Цилиндр будет описанным около пирамиды, когда вершина пирамиды будет принадлежать его одному основанию, а второе основание цилиндра будет описано около основания пирамиды. При этом описать цилиндр около пирамиды можно лишь в том случае, если основанием пирамиды служит вписанный многоугольник (необходимое и достаточное условие).

Пирамиды правильные

Еще один важный подкласс пирамид — это правильные фигуры. Правильной пирамида будет только в том случае, если для нее справедливы следующие два геометрических условия:

• она является прямой;
• ее основание — это n-угольник равносторонний и равноугольный.

Что значит «пирамида прямая», было отмечено в предыдущем пункте. Здесь лишь поясним второе условие. Правильный многоугольник может иметь сколько угодно сторон, начиная с 3-х. Так, правильными являются равносторонний треугольник, квадрат, шестиугольник с одинаковыми длинами сторон и углами по 120o. Заметим, что ромб с одинаковыми сторонами не является правильным, поскольку у него не все углы равны друг другу.

Выше показаны четыре правильные пирамиды, обладающие разными правильными основаниями.

Любые математические расчеты параметров удобно проводить именно для правильных фигур.

Пирамиды

      Рассмотрим произвольную плоскость α , произвольный выпуклый   A₁A₂ … A_n ,   расположенный в этой плоскости, и точку   S ,   не лежащую в плоскости α .

     Определение 1. Пирамидой (n — угольной пирамидой) называют фигуру, образованную отрезками, соединяющими точку  S   со всеми точками многоугольника   A₁A₂ … A_n   (рис. 1) .

     Замечание 1. Напомним, что многоугольник   A₁A₂ … A_n   состоит из   A₁A₂ … A_n   и ограниченной ею части плоскости.

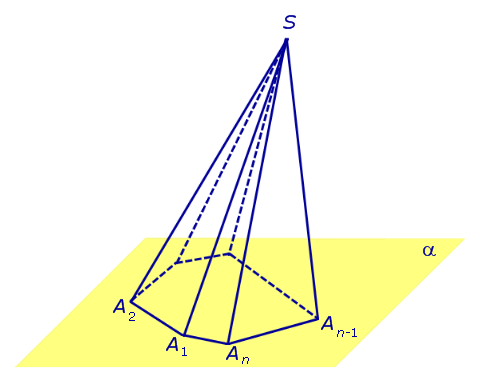
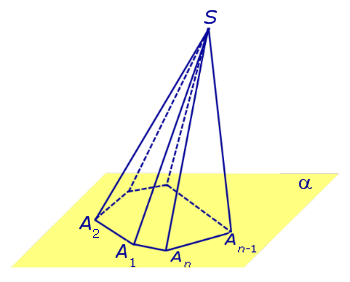
Рис.1

      Определение 2.

	Точку S называют вершиной пирамиды.
	A1A2 … An   называют основанием пирамиды.
	Точки   A1, A2, … , An   называют вершинами основания пирамиды.
	Точки   A1 , A2 , … , An , S   часто называют просто вершинами пирамиды.

α называют высотой пирамиды.

Отрезки   SA₁ , SA₂ , … , SA_n   называют боковыми ребрами пирамиды.

Стороны   A₁A₂ … A_n   называют ребрами основания пирамиды.

Боковые ребра и ребра основания пирамиды часто называют просто ребрами пирамиды.

Треугольники   SA₁A₂ , SA₂A₃ , … , SA_nA₁   называют боковыми гранями пирамиды.

Множество всех боковых граней пирамиды составляет боковую поверхность пирамиды.

Боковые грани и основание пирамиды часто называют просто гранями пирамиды.

Полная поверхность пирамиды состоит из основания пирамиды и ее боковой поверхности.

      Теорема Эйлера. Для любой пирамиды справедливо равенство:

число вершин

+

число граней

–

число ребер

=

2

числовершин

+

числограней

–

числоребер

=

2

числовершин

+

числограней

–

–

числоребер

=

2

      Доказательство. Заметим, что у n — угольной пирамиды   (n + 1)   вершина,   n   боковых граней,   1   основание,   n   ребер основания и   n   боковых ребер. Следовательно, у n — угольной пирамиды   (n + 1)   грань и   2n   ребер.

      Поскольку

(n + 1) + (n + 1) – 2n = 2

то теорема Эйлера доказана.

Формулы для объема, площади боковой и полной поверхности усеченной пирамиды

     Введем следующие обозначения

V	объем
Sбок	площадь
Sполн	площадь
Sверх.осн	площадь верхнего
Sнижн.осн	площадь нижнего
Pверх.осн	периметр верхнего
Pнижн.осн	периметр нижнего

V объем

Sбок площадь

Sполн площадь

Sверх.осн площадь верхнего

Sнижн.осн площадь нижнего

Pверх.осн периметр верхнего

Pнижн.осн периметр нижнего

      Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности усеченной пирамиды:

Пирамида	Рисунок	Формулы для объема, площади боковой и полной поверхности
Произвольная		, гдеh –
		(см. раздел ), , * * * * * * * * * * * * гдеh – ,a  – длина ,a’ – длина ,l – длина

Произвольная

Формулы для объема, площади боковой и полной поверхности: , гдеh –

Формулы для объема, площади боковой и полной поверхности: (см. раздел ), , * * * * * * * * * гдеh  – ,a – длина ,a’ – длина ,l – длина

Прямые и наклонные пирамиды

При рассмотрении вопроса, что такое пирамида, выше было сказано, что в зависимости от числа сторон (углов) многоугольного основания говорят о пирамидах четырехугольной, пятиугольной, треугольной и так далее.

Существует еще одна важная классификация этих фигур: они могут быть прямыми и наклонными. Если из вершины H фигуры провести к основанию перпендикуляр, то в некоторой точке O он пересечет основание пирамиды. Если точка O является геометрическим центром n-угольника, значит, пирамида будет прямой. Если O этим центром не является, то пирамида будет наклонной.

Внешнее различие между этими типами фигур видно с первого взгляда. Наклонная и прямая пирамиды четырехугольные показаны ниже.

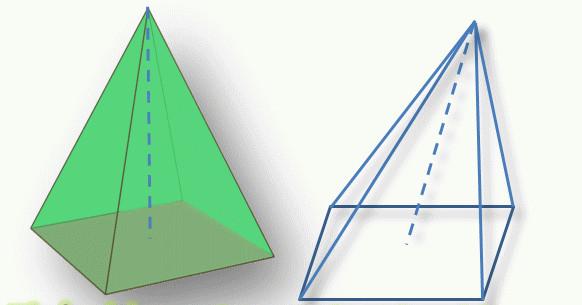
Двоякое использование термина «апофема»

В геометрии значение слова «апофема» или «апотема», как ее еще называют, зависит от того, к какому объекту ее применяют. Существует два принципиально разных класса фигур, в которых она является одной из их характеристик.

В первую очередь это плоские многоугольники. Что такое апофема для многоугольника? Это высота, проведенная из геометрического центра фигуры к любой из ее сторон.

Чтобы было понятнее, о чем идет речь, рассмотрим конкретный пример. Предположим, что имеется правильный шестиугольник, показанный ниже на рисунке.

Символом l обозначена длина его стороны, буквой a — апофема. Для отмеченного треугольника она является не только высотой, но и биссектрисой, и медианой. Несложно показать, что через сторону l ее можно вычислить так:

Аналогичным образом апофема определяется для любого n-угольника.

Во вторую очередь — это пирамиды. Что такое апофема для такой фигуры? Этот вопрос требует более детального рассмотрения.

Тетраэдры. Правильные тетраэдры

      Определение 5. Произвольную называют тетраэдром.

     Утверждение. У любой противоположные ребра попарно .

     Доказательство. Рассмотрим правильную треугольную пирамиду   SABC и пару ее противоположных ребер, например,   AC   и   BS.   Обозначим буквой   D   середину ребра   AC.   Поскольку отрезки   BD   и   SD   являются медианами в равнобедренных треугольниках   ABC   и   ASC,   то   BD   и   SD   перпендикулярны ребру   AC   (рис. 4).

Рис.4

      заключаем, что прямая   AC   перпендикулярна плоскости   BSD.   Следовательно, прямая   AC   перпендикулярна прямой   BS,   что и требовалось доказать.

      Определение 6. , у которой все равны, называют правильным тетраэдром (рис. 5).

Рис.5

     Задача. Найти правильного тетраэдра с ребром   a .

      Решение. Рассмотрим правильный тетраэдр   SABC.   Пусть точка   O   – , опущенного из вершины   S   на плоскость   ABC.   Поскольку   SABC   – , то точка   O   является точкой пересечения медиан равностороннего треугольника   ABC.   ,

где буквой   D   обозначена середина ребра   AC   (рис. 6).

Рис.6

      Так как

,

то

.

      По из треугольника   BSO  находим

.

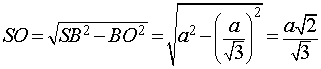      Ответ.

Решение задачи 3

Правильная треугольная пирамида РАВС с высотой  и стороной основания  рассечена плоскостью , проходящей через середину  высоты РН параллельно основанию АВС. Найти площадь боковой поверхности полученной усеченной пирамиды.

Решение. Проиллюстрируем:

Рис. 8. Иллюстрация к задаче 3

АСВ – правильный треугольник, Н – центр данного треугольника (центр вписанной и описанной окружностей). РМ – апофема заданной пирамиды.  – апофема усеченной пирамиды. Согласно свойству параллельных плоскостей (две параллельные плоскости рассекают любую третью плоскость так, что линии пересечения параллельны), имеем несколько пар подобных треугольников с равным коэффициентом подобия. В частности нас интересует отношение:

Отсюда:

Найдем НМ. Это радиус окружности, вписанной в основание, соответствующая формула нам известна:

Теперь из прямоугольного треугольника РНМ по теореме Пифагора найдем РМ – апофему исходной пирамиды:

Из начального соотношения:

Теперь нам известны все элементы для нахождения площади боковой поверхности усеченной пирамиды:

Итак, мы ознакомились с понятиями усеченной пирамиды и правильной усеченной пирамиды, дали основные определения, рассмотрели свойства, доказали теорему о площади боковой поверхности. Следующий урок будет посвящен решению задач.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/mnogogranniki/piramida-pravilnaya-i-usechyonnaya-piramidy

https://www.youtube.com/watch?v=3SNed3CCsZs

Усеченная пирамида

http://1.bp.blogspot.com/-mVfd5cZ9sMo/T1TPcqgVyQI/AAAAAAAAA9o/rq9cdW1KM1s/s1600/Geom_17.jpg

http://infourok.ru/zadaniya_dlya_ustnogo_scheta_po_temeusechennaya_piramida_geometriya_10_klass-566065.htm

http://www.otbet.ru/book/class-10/geometria/uchebnik-glazkov-yu-a-testy-po-geometrii/

http://5klass.net/geometrija-10-klass/Piramidy/001-Piramida.html

http://interneturok.ru/ru/school/geometry/10-klass/mnogogranniki/usechennaya-piramida
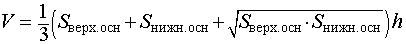