Преобразование графиков функций у= f(x) в y=-f(x); y=f(-x); y=-f(-x); y=f(x-a); y=f(x)+b; y=f(ax); y=kf(x); y=

Способы задания функции.

Числовые функции чаще всего задаются при помощи формул. Такой способ задания называют аналитическим. Например, функции \(y=x^2, \ y=|x|^{3/2}, \ y=\sin^3{3x}\) заданы на множестве \(\mathbb{R}\) аналитически.

Если числовая функция f задана формулой и не указана область ее определения \(D(f)\) , то принято считать, что \(D(f)\) — множество всех тех значений аргумента, при которых эта формула имеет смысл, и результатом каждой операции, указанной в формуле, является вещественное число. Например, если \(f(x)=\sqrt{9-x^2}\), то \(D(f)=\), а если \(f(x)=\sqrt{\operatorname{lg} \sin{x}}\), то \(D(f)\) — множество корней уравнения \(\sin x=1\) то есть множество чисел \(x_{k}=\pi/2.+2\pi k\), где \(k\in Z\).

Следует отметить, что функция может быть задана различными формулами на разных промежутках. Например, функция
$$
f(x)=\left\{\begin{array}{l}-x,\quad если\;x\;<\;0,\\x^{2},\quad если\;0\leq x\leq1,\\2-\sqrt{x},\quad если\;x>1,\end{array}\right.\nonumber
$$
задана аналитическим способом на \(\mathbb{R}\) с помощью трех различных формул.

Иногда функциональная зависимость описывается с помощью таблицы, содержащей лишь некоторые значения аргумента и соответствующие значения функции. Для значений аргумента, не содержащихся в таблице, значения функции обычно находят приближенно.

На практике часто соответствие между значениями аргумента и значениями функции задается с помощью рисунка. Например, в медицине при изучении работы сердца получают электрокардиограммы — кривые, отражающие изменение с течением времени электрических импульсов в мышце сердца. В практике физических измерений функциональная зависимость часто задается с помощью эскиза графика, снимаемого, например, с экрана осциллографа.

Степенная функция с целым показателем

Для начала введем понятие степени с целым показателем.

Определение 3

Степень действительного числа $a$ c целым показателем $n$ определяется формулой:

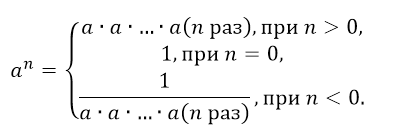
Рисунок 4.

Рассмотрим теперь степенную функцию с целым показателем, её свойства и график.

Определение 4

$f\left(x\right)=x^n$ ($n\in Z)$ называется степенной функцией с целым показателем.

Если степень больше нуля, то мы приходим к случаю степенной функции с натуральным показателем. Его мы уже рассмотрели выше. При $n=0$ мы получим линейную функцию $y=1$. Её рассмотрение оставим читателю. Осталось рассмотреть свойства степенной функции с отрицательным целым показателем

Обзор основных элементарных функций

Все элементарные функции можно представить в виде конечного числа операций сложения, вычитания, умножения и деления, произведенных над выражением вида:. Обратные функции могут выражаться также через логарифмы. Ниже перечислены основные элементарные функции.

Степенная функция:, где — показатель степени. Она зависит от основания степени . Обратной к степенной функции является также степенная функция:. При целом неотрицательном значении показателя она является многочленом. При целом значении – рациональной функцией. При рациональном значении – иррациональной функцией.

Трансцендентные функции

Показательная функция:, где — основание степени. Она зависит от показателя степени . Обратная функция — логарифм по основанию .

Экспонента, е в степени х:, Это показательная функция, производная которой равна самой функции:. Основанием степени экспоненты является число . Обратная функция — натуральный логарифм — логарифм по основанию числа .

Тригонометрические функции:Синус:   ;Косинус:   ;Тангенс:   ;Котангенс:   ; Здесь — мнимая единица, .

Обратные тригонометрические функции: Арксинус:   ,   ; Арккосинус:   ,   ; Арктангенс:   ,   ; Арккотангенс:   ,   .

Гиперболические функции: Гиперболический синус:   ; Гиперболический косинус:   ; Гиперболический тангенс:   ; Гиперболический котангенс:   .

Обратные гиперболические функции: Ареасинус:   ; Ареакосинус:   ; Ареатангенс:   ; Ареакотангенс:   .

Дифференцирование показательной функции

Для дифференцирования показательной функции, ее основание нужно привести к числу , применить таблицу производных и правило дифференцирования сложной функции.

Для этого нужно использовать свойство логарифмов и формулу из таблицы производных:.

Пусть задана показательная функция:. Приводим ее к основанию Применим правило дифференцирования сложной функции. Для этого вводим переменную Тогда Из таблице производных имеем (заменим переменную на ):. Поскольку – это постоянная, то производная по равна. По правилу дифференцирования сложной функции:.

Пример дифференцирования показательной функции

Найти производную функции

Решение

Выразим основание показательной функции через число . Тогда. Вводим переменную. Тогда Из таблицы производных находим:. Поскольку – это постоянная, то производная по равна:. По правилу дифференцирования сложной функции имеем:.

Ответ

Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.

Основные свойства функции :

Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: , то есть для любого значения «икс» существует значение синуса.

Область значений: . Функция  является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает:  или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:,  Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.

График косинуса

Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси  на  влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси  , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .

Графики тангенса и котангенса

Построим график функции

Основные свойства функции :

Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.

Область определения:  – все действительные числа, кроме …  , , , … и т. д. или коротко: , где  – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.

Область значений: . Функция  не ограничена. В этом легко убедиться и аналитически: – если мы приближаемся по оси  к значению  справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте . – если мы приближаемся по оси  к значению  слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .

Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .

В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.

Определение

Степенная функция с показателем степени

– это функция  , значение которой в точке равно значению показательной функции с основанием в точке . Кроме этого,    при  .

Для натуральных значений показателя , степенная функция есть произведение чисел, равных . Она определена для всех действительных .

Для положительных рациональных значений показателя , степенная функция есть произведение корней степени из числа . Для нечетных , она определена для всех действительных . Для четных , степенная функция определена для неотрицательных .

Для отрицательных , степенная функция определяется по формуле:. Поэтому она не определена в точке .

Для иррациональных значений показателя , степенная функция определяется по формуле:, где – произвольное положительное число, не равное единице:  . При , она определена для . При , степенная функция определена для .

Непрерывность. Степенная функция непрерывна на своей области определения.

Обратная функция.

Пусть задана числовая функция \(y=f(x),\;x\in D(f)\). Тогда каждому числу \(x_0\in D(f)\)соответствует единственное число \(y_{0}=f(x_{0})\in E(f)\) . Нередко приходится по заданному значению функции \(y_0\) находить соответствующее значение аргумента, то есть решать относительно \(x\) уравнение
$$
f(x)=y_{0},\quad y_{0}\in E(f).\label{ref8}
$$

Это уравнение может иметь не одно, а несколько и даже бесконечно много решений. Решениями уравнения \eqref{ref8} являются абсциссы всех точек, в которых прямая \(y=y_0\) пересекает график функции \(y=f(x)\).

Например, если \(f(x)=x^{2}\), то уравнение
$$
x^{2}=y_{0},\quad y_{0}>0,\nonumber
$$
имеет два решения: \(x_{0}=\displaystyle \sqrt{y_0}\) и \({\widetilde x}_0=\sqrt{y_0}\). Если \(f(x)=\sin x\), то уравнение
$$
\sin{x}=y_{0},\quad |y_{0}|\leq 1,\nonumber
$$
имеет бесконечно много решений вида \(x_n=(-1)^{n}x_{0}+\pi n\), где \(n\in\mathbb{Z}\;x_0\) — одно из решений этого уравнения.

Однако существуют функции, для которых уравнение \eqref{ref8} при каждом \(y_{0}\in E(f)\) однозначно разрешимо, то есть имеет единственное решение \(x_0\in D(f)\). Этим свойством обладают, например, следующие функции:

1. \(f(x)=3x+4,\;D(f)=\mathbb{R}\);
2. \(f(x)=x^{3},\;D(f)=\mathbb{R}\);
3. \(f(x)=\displaystyle \frac{1}{x},\quad D(f)=\{x\in\mathbb{R},\;x\neq 0\}\).

Если функция \(f\) такова, что при каждое значение \(y_{0}\in E(f)\) она принимает только при одном значении \(x_{0}\in D(f)\) , то эту функцию называют обратимой. Для такой функции уравнение
$$
f(x)=y\nonumber
$$
можно при любом \(у\in Е(f)\)однозначно разрешить относительно \(x\), то есть каждому \(y\in Е(f)\) соответствует единственное значение \(x\in D(f)\).

Это соответствие определяет функцию, которую называют обратной к функции \(f\) и обозначают символом \(f^{-1}\).

Заметим, что прямая \(y=y_0\) для каждого \(y_{0}\in E(f)\) пересекает график обратимой функции \(y=f(x)\) в единственной точке \((x_0,\;y_0)\), где \(f(x_{0})=y_{0}\).

Обозначая, как обычно, аргумент обратной функции буквой \(x\), а ее значения — буквой \(y\), обратную для \(f\) функцию записывают в виде
$$
y=f^{-1}(x),\quad x\in D(f^{-1}).\nonumber
$$

Для упрощения записи вместо символа \(f^{-1}\) будем употреблять букву \(g\).

Отметим следующие свойства, которые показывают, как связаны данная функция и обратная к ней:

1. если \(g\) — функция, обратная к \(f\), то и \(f\) — функция, обратная к \(g\); при этом
   $$
   D(g)=E(f),\quad E(g)=D(f),\nonumber
   $$
   то есть область определения функции \(g\) совпадает с множеством значений функции \(f\) и наоборот;
2. для любого \(x\in D(f)\) справедливо равенство
   $$
   g(f(x))=x,\nonumber
   $$
   а для любого \(х\in Е(f)\) справедливо равенство
   $$
   f(g(x))=x;\nonumber
   $$
3. график функции \(y=g(x)\) симметричен графику функции \(y=f(x)\) относительно прямой \(y=x\);
4. если нечетная функция обратима, то обратная к ней функция также является нечетной;
5. если \(f\) — строго возрастающая (строго убывающая) функция, то она обратима, причем обратная к ней функция \(g\) также является строго возрастающей (строго убывающей).

Рис. 9.9

Свойства 1) и 2) следуют непосредственно из определения обратной функции, 4) и 5) — из определений обратной и соответственно нечетной и строго монотонной функции.

Рис. 9.10

Рассмотрим свойство 3). Пусть точка \((x_{0},y_{0})\) принадлежит графику функции \(y=f(x)\), то есть \(y_{0}=f(x_0)\). Тогда \(x_{0}=g(y_{0})\), то есть точка \((x_{0},y_{0})\) принадлежит графику обратной функции \(g\). Так как точки \((x_{0},y_{0})\) и \((y_{0},x_{0})\) симметричны относительно прямой \(y=x\) (рис. 9.9), то график функции \(у=g(х)\) симметричен графику функции относительно этой прямой.

Рис. 9.11

На рис. 9.10 изображены графики взаимно обратных функций \(y=x^{2},\;x\geq 0\), и \(y=\sqrt{x}\), а на рис. 9.11 — графики взаимно обратных функций \(y=x^{2},\;x\leq 0\), и \(y=-\sqrt{x}\).

2. Функция у=х, теорема о симметрии графиков функций

Опре­де­ле­ние:

Функ­ци­ей на­зы­ва­ет­ся закон со­от­вет­ствия, по ко­то­ро­му каж­до­му зна­че­нию ар­гу­мен­та х ста­вит­ся в со­от­вет­ствие един­ствен­ное зна­че­ние функ­ции у.

Рас­смот­рим ис­сле­ду­е­мую функ­цию при : 

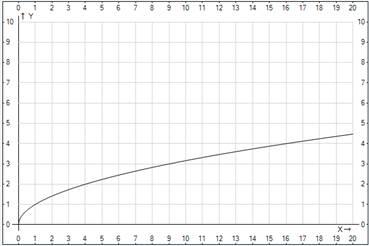
Рис. 1. Гра­фик функ­ции 

Оче­вид­но, что пред­став­лен­ный гра­фик (Рис. 1.) про­хо­дит через точки (1;1), (4;2), (9;3) и т. д.

Чтобы из­ба­вить­ся от корня, воз­ве­дем функ­цию в квад­рат, на­ло­жив усло­вие на у:

Рас­смот­рим две функ­ции. Пер­вая –  при , гра­фик ее – это часть па­ра­бо­лы. Вто­рая функ­ция –  при , это также часть па­ра­бо­лы. Дан­ные ветви па­ра­бол сим­мет­рич­ны от­но­си­тель­но пря­мой . гра­фи­ки имеют две общие точки: (0;0) и (1;1). На ветви па­ра­бо­лы  лежат точки с ко­ор­ди­на­та­ми , на ветви па­ра­бо­лы  – точки с ко­ор­ди­на­та­ми . Эти точки сим­мет­рич­ны от­но­си­тель­но пря­мой . Рис. 2.

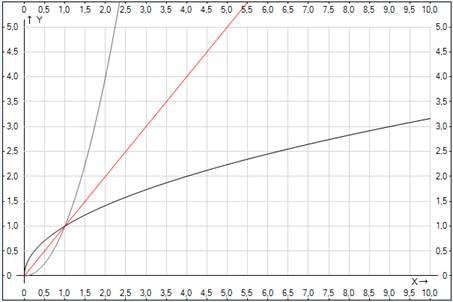
Рис. 2. Гра­фи­ки функ­ций ,  и 

Тео­ре­ма:

Точки А(а;b) и В(b,a) сим­мет­рич­ны от­но­си­тель­но пря­мой .

До­ка­за­тель­ство:

Рас­смот­рим чер­теж (ри­су­нок 3). Ко­ор­ди­на­ты точки А озна­ча­ют, что пря­мо­уголь­ный тре­уголь­ник  имеет ка­те­ты а и b. Ана­ло­гич­но тре­уголь­ник  имеет те же самые ка­те­ты. Таким об­ра­зом, рас­смот­рен­ные тре­уголь­ни­ки равны, и из их ра­вен­ства сле­ду­ет ра­вен­ство углов 1 и 2 и ра­вен­ство ги­по­те­нуз ОА и ОВ. На­пом­ним, что пря­мая  яв­ля­ет­ся бис­сек­три­сой, от­сю­да углы  и  со­став­ля­ют по , таким об­ра­зом, углы 3 и 4 равны (т. к. равны углы 1 и 2). От­сю­да ОН – бис­сек­три­са в рав­но­бед­рен­ном тре­уголь­ни­ке . Бис­сек­три­са, как из­вест­но, яв­ля­ет­ся осью сим­мет­рии для всего тре­уголь­ни­ка, в том числе и для ин­те­ре­су­ю­щих нас точек А и В.

Рис. 3. Чер­теж к тео­ре­ме

До­ка­зан­ная тео­ре­ма поз­во­ля­ет сде­лать вывод для лю­бо­го n:

Гра­фик функ­ции  при  сим­мет­ри­чен гра­фи­ку функ­ции  при  от­но­си­тель­но пря­мой .

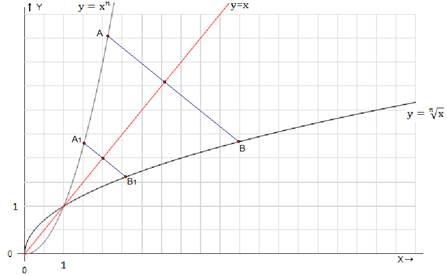
Рис. 4. Обоб­ще­ние тео­ре­мы

Исследование графика функции

Для периодических функций идет исследование графика функции только на промежутке периода

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

• Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
• Умеет определять точки пересечения графика функции с осями координат: Да
• Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
• Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
• Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
• Горизонтальные асимптоты графика функции: Да
• Наклонные асимптоты графика функции: Да
• Четность и нечетность функции: Да

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

e

e число, которое примерно равно 2.7

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

pi

Число — «Пи», которое примерно равно 3.14

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7.5, не 7,5

2*x

— умножение

3/x

— деление

x^3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

Другие функции:

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

Ограниченные и неограниченные функции.

Функцию f называют ограниченной снизу на множестве \(X\subset D(f)\), если существует число \(С_1\) такое, что для любого \(x\in X\) выполняется неравенство \(f(x) \geq C_1\).

Используя символы \(\exists\) и \(\forall\), это определение можно записать так:
$$
\exists C_{1}:\forall x\in X\rightarrow f(x)\geq C_{1}.\nonumber
$$
Аналогично функцию f называют ограниченной сверху на множестве \(X\subset D(f)\), если
$$
\exists C_{2}:\forall x\in X\rightarrow f(x)\leq C_{2}.\nonumber
$$

Функцию, ограниченную и сверху, и снизу на множестве X, называют ограниченной на этом множестве.

Функция f является ограниченной на множестве X тогда и только тогда, когда
$$
\exists c>0:\forall x\in X\rightarrow|f(x)|\leq C.\label{ref4}
$$

Если неравенство \(|f(x)|\leq C\) выполняется для всех \(x\in D(f)\), говорят, что функция f ограничена.

Геометрически ограниченность функции f на множестве X означает, что график функции \(y=f(x), x\in X,\) лежит в полосе \({-C\leq y\leq C}.\)

Например, функция \(y=\displaystyle \sin\frac{1}{x}\), определенная при \(x\in\mathbb{R}, x\neq 0\), ограничена, так как
$$
|\sin\frac{1}{x}|\leq 1\nonumber
$$

Функция f не ограничена на множестве X, если условие \eqref{ref4} не выполняется, то есть
$$
\forall C>0\ \exists x_{C}\in X:|f(x_{C})|\geq C.\label{ref5}
$$

Если \(X= D(f)\) и выполнено условие \eqref{ref5}, то говорят, что функция f не ограничена.

Пример 8

Доказать, что функция \(y=\displaystyle \frac{1}{x^{2}}\) не ограничена.

\(\triangle\) Функция \(\displaystyle \frac{1}{x^{2}}\) определена при \(x\in\mathbb{R}\), \(x\neq 0\). Пусть C — любое положительное число, и пусть \(\displaystyle {x_{C}=\frac{1}{\sqrt{2C}}}\), тогда \(\displaystyle y(x_{C})=2C>C\) то есть выполняется условие \eqref{ref5}. \(\blacktriangle\)

Пусть Y — множество значений, которые функция f принимает на множестве \(X\subset D(f)\) . Тогда точную верхнюю грань множества Y называют точной верхней гранью функции f на множестве X и обозначают \(\sup_{x\in X}{f(x)}\), а точную нижнюю грань множества Y — точной нижней гранью функции f на множестве X и обозначают \(\displaystyle \inf_{x\in X}{f(x)}\).
Если X=D(f), то в этих определениях указание на множество X опускают.

Пусть существует точка \(x_{0}\in X\subset D(f)\) такая, что для всех \(x\in X\) выполняется неравенстве \(f(x) \leq f(x_0)\).Тогда говорят, что функция f принимает в точке \(x_{0}\) наибольшее (максимальное) значение на множестве X и пишут \(f(x_{0})=\displaystyle \max_{x\in X}f(x)\) В этом случае \(\displaystyle \sup_{x\in X}{f(x)}=f(x_{0}) \)

Аналогично, если \(\exists x_{0}\in X\subset D(f):\forall x\in X\rightarrow f(x)\geq f(x_{0})\) , то говорят, что функция f принимает в точке \(x_0\) наименьшее (минимальное) значение на множестве X, и пишут \(f(x_{0})=\displaystyle \min_{x\in X}f(x)\). В этом случае \(\displaystyle \inf_{x\in X}f(x)=f(x_{0})\).

Максимальные и минимальные значения называют экстремальными.

Например, если \(f(x)=\sin x\), то \(\displaystyle \sup_{x\in\mathbb{R}}f(x)=\max_{x\in\mathbb{R}}f(x)=f(x_{k})\), где \(x_{k}=\displaystyle \frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z},\;\inf_{x\in\mathbb{R}}f(x)=\min_{x\in\mathbb{R}}{f}(x)=f(\widetilde{x}_{k}),\) где \(\widetilde{x}_{k}=-\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z}\).

6. Функция y=ⁿ√x при нечетных n, свойства в общем и частных случаях

Пе­рей­дем к функ­ци­ям  для нечет­но­го n, т. е. функ­ци­ям  и т. д., при­чем в дан­ном слу­чае  и . Рис. 3.

Рис. 3. Гра­фик функ­ции  для нечет­но­го n, 

Если ар­гу­мент ме­ня­ет­ся от минус бес­ко­неч­но­сти до плюс бес­ко­неч­но­сти, функ­ция воз­рас­та­ет от минус бес­ко­неч­но­сти до плюс бес­ко­неч­но­сти.

Ос­нов­ные свой­ства рас­смат­ри­ва­е­мых функ­ций:

1.      Об­ласть опре­де­ле­ния: ;

2.      Об­ласть зна­че­ний: ;

3.      Гра­фи­ки функ­ций про­хо­дят через точки (0;0), (1;1), (-1;-1)

4.      Функ­ции нечет­ные, гра­фи­ки сим­мет­рич­ны от­но­си­тель­но на­ча­ла ко­ор­ди­нат;

5.      Функ­ции воз­рас­та­ют от минус до плюс бес­ко­неч­но­сти.

Рас­смот­рим вза­им­ное рас­по­ло­же­ние двух кри­вых: . Рис. 4.

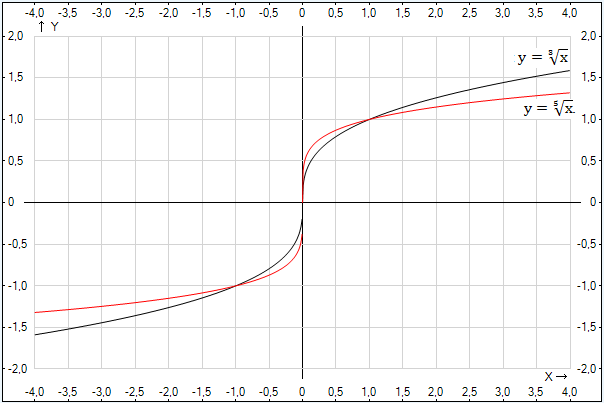
Рис. 4. Вза­им­ное рас­по­ло­же­ние гра­фи­ков функ­ций 

На участ­ке  кри­вая  на­хо­дит­ся выше кри­вой , од­на­ко когда  кри­вые рас­по­ла­га­ют­ся на­о­бо­рот,  рас­по­ло­же­на выше :

Неявные функции. Параметрически заданные функции.

Пусть Е — множество точек \(M(x,y)\) плоскости \(Oxy\). Если каждой точке \(M\in E\) поставлено в соответствие по некоторому правилу (закону) число z, то говорят, что на множестве E задана числовая функция от переменных \(x\) и \(y\), и пишут \(z=f(x,y),\;(x,y)\in E\).

Например, объем конуса \(v\) есть функция от переменных r и h, где r — радиус основания, h — высота конуса. Эта функция задается формулой \(v=\displaystyle \frac{1}{3}\pi r^{2}h\).

Аналогично вводится понятие функции от трех и большего числа переменных.

Пусть функция \(F(x,y)\) определена на некотором множестве точек плоскости. Рассмотрим уравнение
$$
F(x,y)=0.\label{ref9}
$$

Рис. 9.12

Графиком уравнения \eqref{ref9} в прямоугольной системе координат называют множество всех точек плоскости, координаты которых удовлетворяют этому уравнению. Например, графиком уравнения
$$
x^{2}+y^{2}-1=0\label{ref10}
$$
является единичная окружность (рис. 9.12).

Естественной является постановка вопроса о том, можно ли уравнение \eqref{ref9} однозначно разрешить относительно \(y\), то есть найти единственную функцию \(y=f(x)\) такую, что \(F(x,f(x))=0\), где \(x\) принимает значения из некоторого промежутка.

Обратимся к уравнению \eqref{ref10}. Если \(|x|>1\), то не существует значений \(y\) таких, что пара чисел \((x,y)\) удовлетворяет уравнению \eqref{ref10}. Если \(|x|\leq 1\), то, решая это уравнение относительно y, получаем
$$
y=\pm\sqrt{1-x^{2}}.\label{ref11}
$$

Таким образом, если \(|x|\;<1\), то из уравнения \eqref{ref10} \(y\) выражается через \(х\) неоднозначно: каждому значению \(x\) соответствуют два различных значения \(y\), а именно \(y_{1}=-\sqrt{1-x^{2}}\quad y_{2}=\sqrt{1-x^{2}}\quad (y_{1}=y_{2}\) при \(x=-1\;x=1)\).

Отсюда следует, что всякая функция \(y=f(x)\), которая в точке \(x\in\) принимает либо значение \(y_{1}\), либо значение \(y_{2}\), удовлетворяет уравнению \eqref{ref10}, то есть
$$
x^{2}+f^{2}(x)-1=0,\quad x\in.\nonumber
$$

Например, функция \(y=f(x)\), принимающая значение \(y_1\) при \(x\in\), удовлетворяет уравнению \eqref{ref10}. Меняя \(\alpha\), можно получить бесконечное множество функций, удовлетворяющих на отрезке \(\) уравнению \eqref{ref10}.

Будем теперь рассматривать уравнение \eqref{ref10} в прямоугольнике
$$
K_{1}=\{(x,y):-1\leq x\leq 1,\;0\leq y\leq 1\}.\nonumber
$$

В этом случае существует единственная функция \(y=y_{1}=\sqrt{1-x^{2}},\;-1\leq x\leq 1\), удовлетворяющая уравнению \eqref{ref10} и такая, что \(y\in\). Эту функцию называют неявной функцией, определяемой уравнением \eqref{ref10} в прямоугольнике \(K_1\).

Аналогично в прямоугольнике \(K_{1}=\{(x,y):-1\leq x\leq 1,\;-1\leq y\leq 0\}\) неявная функция, определяемая уравнением \eqref{ref10}, задается формулой \(y=y_{2}=-\sqrt{1-x^{2}},\;-1\leq x\leq 1\).

Вернемся к уравнению \eqref{ref9}. Пусть прямоугольник \(K=\{(x,y):|x-x_{0}|\leq a,\;|y-у_0|\leq b\) содержится в области определения функции \(F(х,у)\), и пусть \(F(х_0,y_0)=0\). Если на отрезке \(\Delta=\lceil x_{0}-a,x_{0}+a\rceil\) существует единственная функция \(y=f(x)\) такая, что \(f(x)\in\lceil y_0-b,y_0+b\rceil\) и
$$
F(x,f(x))=0,\quad x\in\Delta,\nonumber
$$
то говорят, что уравнение \eqref{ref9} определяет в прямоугольнике \(K\) переменную y как неявную функцию переменной \(x\).

Достаточные условия существования неявной функции и другие вопросы, связанные с неявными функциями, рассматриваются далее в параграфе 28.

Функция одной переменной может быть задана не только в явном виде \(y=f(x)\) или неявно уравнением \(F(х,у)=0\), но также параметрически. Этот способ задания состоит в следующем.

Пусть функции \(x=\varphi(t)\) и \(\varphi(t)\) определены на некотором множестве \(E\), и пусть \(E_1\) — множество значений функции \(\varphi\). Предположим, что функция \(\varphi\) обратима на множестве \(E\), и пусть \(t=\varphi^{-1}(x)\) — обратная к ней функция. Тогда на множестве \(E_1\) определена сложная функция \(y=\psi(\varphi^{-1}(x))=f(x)\), которую называют параметрически заданной формулами (уравнениями) \(х=\varphi(t),\quad y=\psi(t)\).

Например, уравнениях \(x=\cos t,\;y=\sin t\), где \(t\in\left \), определяют параметрически заданную функцию \(y=f(x)\). В данном случае \(t=\arccos x,\;y=\sin(\arccos x)=\sqrt{1-x^{2}}\).

Тригонометрические функции, их свойства и графики.

Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.

Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода , где Т — период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.

Теперь разберемся со всеми тригонометрическими функциями по порядку.

Функция синус y = sin(x).

Изобразим график функции синус, его называют «синусоида».

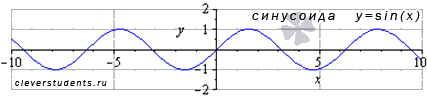
Свойства функции синус y = sinx.

• Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при .
• Наименьший положительный период функции синуса равен двум пи: .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть .
• Функция синус — нечетная, так как .
• Функция убывает при ,
  возрастает при .
• Функция синус имеет локальные максимумы в точках ,
  локальные минимумы в точках .
• Функция y = sinx вогнутая при ,
  выпуклая при .
• Координаты точек перегиба .
• Асимптот нет.

Функция косинус y = cos(x).

График функции косинус (его называют «косинусоида») имеет вид:

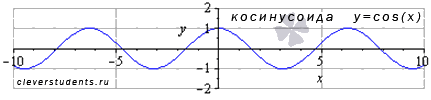
Свойства функции косинус y = cosx.

• Область определения функции косинус: .
• Наименьший положительный период функции y = cosx равен двум пи: .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Область значений функции косинус представляет интервал от минус единицы до единицы включительно: .
• Функция косинус — четная, так как .
• Функция убывает при ,
  возрастает при .
• Функция y = cosx имеет локальные максимумы в точках ,
  локальные минимумы в точках .
• Функция вогнутая при ,
  выпуклая при .
• Координаты точек перегиба .
• Асимптот нет.

Функция тангенс y = tg(x).

График функции тангенс (его называют «тангенсоида») имеет вид:

Свойства функции тангенс y = tgx.

• Область определения функции тангенс: , где , Z – множество целых чисел.
  Поведение функции y = tgx на границе области определения
  Следовательно, прямые , где , являются вертикальными асимптотами.
• Наименьший положительный период функции тангенс .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Область значений функции y = tgx: .
• Функция тангенс — нечетная, так как .
• Функция возрастает при .
• Функция вогнутая при ,
  выпуклая при .
• Координаты точек перегиба .
• Наклонных и горизонтальных асимптот нет.

Функция котангенс y = ctg(x).

Изобразим график функции котангенс (его называют «котангенсоида»):

Свойства функции котангенс y = ctgx.

• Область определения функции котангенс: , где , Z – множество целых чисел.
  Поведение на границе области определения
  Следовательно, прямые , где являются вертикальными асимптотами.
• Наименьший положительный период функции y = ctgx равен пи: .
• Функция обращается в ноль при , где , Z – множество целых чисел.
• Область значений функции котангенс: .
• Функция нечетная, так как .
• Функция y = ctgx убывает при .
• Функция котангенс вогнутая при ,
  выпуклая при .
• Координаты точек перегиба .
• Наклонных и горизонтальных асимптот нет.

Выражения через комплексные числа

Рассмотрим функцию комплексного переменного . Выразим комплексную переменную через модуль и аргумент   ( ): . Комплексное число представим в виде действительной и мнимой частей:. Имеем: Далее учтем, что аргумент определен не однозначно:,

Рассмотрим случай, когда , то есть показатель степени — действительное число, .   Тогда .

Если — целое, то и — целое. Тогда, в силу периодичности тригонометрических функций:. То есть показательная функция при целом показателе степени, для заданного , имеет только одно значение и поэтому является однозначной.

Если — иррациональное, то произведения ни при каком не дают целого числа. Поскольку пробегает бесконечный ряд значений , то функция имеет бесконечно много значений. Всякий раз, когда аргумент получает приращение (один оборот), мы переходим на новую ветвь функции.

Если — рациональное, то его можно представить в виде:, где — целые, не содержащие общих делителей. Тогда. Первые величин, при , дают различных значений . Однако последующие величины дают значения, отличающиеся от предыдущих на целое число. Например, при имеем:. Тригонометрические функции, аргументы которых различаются на величины, кратные , имеют равные значения. Поэтому при дальнейшем увеличении мы получаем те же значения , что и для .

Таким образом, показательная функция с рациональным показателем степени является многозначной и имеет значений (ветвей). Всякий раз, когда аргумент получает приращение (один оборот), мы переходим на новую ветвь функции. Через таких оборотов мы возвращаемся на первую ветвь, с которой начинался отсчет.

В частности, корень степени имеет значений. В качестве примера рассмотрим корень – й степени действительного положительного числа . В этом случае , . . Так, для квадратного корня, , . Для четных . Для нечетных . То есть квадратный корень имеет два значения:   +   и   – .

Использованная литература: И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.