Демонстрационные варианты и задания олимпиады
Содержание:
Олимпиада по математике. 11 класс.
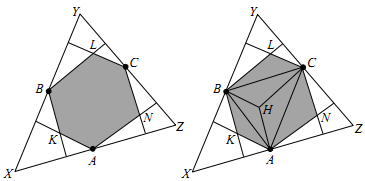
Задача 1 : В игре участвуют два игрока А и Б. Игрок А задаёт значение одного из коэффициентов a, b или c многочлена x3 + ax2+ bx + c. Игрок Б указывает значение любого из двух оставшихся коэффициентов. Затем игрок А задаёт значение последнего коэффициента. Существует ли стратегия игрока А такая, что как бы ни играл игрок Б, уравнениеx3 + ax2 + bx + c = 0 имеет три различных (действительных) решения? Задача 2 : Пусть f(x) = (…((x – 2)2 – 2)2 – 2)2… – 2)2(здесь скобок ( ) – n штук). Найдитеf І(0)Задача 3 :Числа a , b и c таковы , что a2 + b2 + c2 = 1.Докажите, что a4 + b4 + c4 + 2(ab2 + bc2 + ca2)2Ј 1. При каких a, b и c неравенство превращается в равенство?Задача 4 :Пусть прямая L перпендикулярна плоскости P. Три сферы попарно касаются друг друга так, что каждая сфера касается плоскости P и прямой L. Радиус большей сферы равен 1 . Найдите минимальный радиус наименьшей сферы.Задача 5 : На валютной бирже острова Удача продают динары (D), гульдены (G), реалы (R) и талеры (T). Биржевые маклеры имеют право совершить сделку купли-продажи с любой парой валют не более одного раза за день. Курсы валют такие: D = 6G, D = 25R, D = 120 T, G = 4R, G = 21T, R = 5T. Например, запись D = 6G означает,что 1 динар можно купить за 6 гульденов (или 6 гульденов можно продать за 1 динар). Утром у маклера было 80 динаров, 100 гульденов, 100 реалов и 50400 талеров. Вечером у него было одинаковое число динаров и талеров. Каково максимальное значение этого числа?Задача 6 : Известно, что n-вершинник содержит внутри себя многогранник M с центром симметрии в некоторой точке Q и сам содержится в многограннике, гомотетичном M, с центром гомотетии в точке Q и коэффициентом k. Найдите наименьшее значение k, если а) n = 4, b) n = 5Задача 7 : Докажите, что существуют арифметические прогрессии произвольной длины, состоящие из различных попарно взаимно простых натуральных чисел.Задача 8 : Докажите, что плоскость, делящая в одинаковом отношении площадь поверхности и объем описанного многогранника проходит через центр вписанной в этот многогранник сферы.Задача 9 : В треугольнике ABC угол A равен a, а угол B равен 2a. Окружность с центром в точке C радиуса CA пересекает прямую, содержащую биссектрису внешнего угла при вершине B в точках M и N. Найдите углы треугольника MAN.
Олимпиадные задачи по математике 11 класс: Математическая олимпиада физтехаВарианты заданий с решением и ответами : 1 вариант | 2 вариант | 3 вариант
Всероссийская олимпиада по математике |
Международная олимпиада по математике | ЕГЭ по математике
Для знатоков истории
Олимпиада «Музеи. Парки. Усадьбы»
В олимпиаде «Музеи. Парки. Усадьбы» могут принять участие дошкольники и ученики 1–11-х классов индивидуально или в команде. Для ребят, которые хорошо выступили в основном туре, проходит призовая игра: им нужно выполнять задания в ходе интеллектуальной игры-прогулки по Москве. Цель олимпиады «Музеи. Парки. Усадьбы» —не столько проверить знания школьников, сколько помочь им узнать что-то новое, расширить кругозор. Зарегистрироваться можно до 15 марта. Основной тур олимпиады проходит до 31 марта.
Метапредметная олимпиада «Не прервется связь поколений — 2020»
В этом году, помимо учеников шестых — восьмых и 9–11-х классов, в олимпиаде «Не прервется связь поколений» впервые примут участие ребята из четвертых — пятых классов. Им предстоит провести исследовательские работы на темы «Памятник герою», «Реликвия моей семьи», «Хранители памяти: экспонат школьного музея», «Мой герой», «Места памяти», «Имя героя в названии моей школы». Получить подробную информацию и зарегистрироваться можно на сайте олимпиады.

Способы подготовки к олимпиадам
Выберете подход, близкий вам по духу, или сочетайте все три.
Самоподготовка
Тренируйтесь решать математические задачи разной сложности. Для этого вам пригодятся варианты олимпиад прошлых лет или сборники задач. Не забывайте про учебники: школьных будет мало, но можно обратиться к вузовским.
С репетитором
Педагог может помочь составить план подготовки к математической олимпиаде и разъяснить непонятные моменты. Но не стоит забывать о самостоятельной подготовке. Занятия будут продуктивнее, если приходить к репетитору с конкретными вопросами.
Онлайн-школа
Подготовка через интернет удобна тем, что не нужно тратить время на дорогу и можно заниматься где угодно. В домашней онлайн-школе «Фоксфорда» подготовка к олимпиадам входит в индивидуальный маршрут учащихся.
Для поклонников математики в «Домашней школе Фоксфорда» разработан специальный математический маршрут. Там на олимпиадных курсах преподаватели из ведущих вузов страны разбирают сложные задачки и рассказывают о специфике «Ломоносова», ПВГ и других математических олимпиад.
Олимпиадные задания по математике 9 — 11 класс
Олимпиадные задания по математике 9 класс 1. Корень из числа 49 можно извлечь по такой «формуле»: ? 49 = 4 + ?9. Существуют ли другие двузначные числа, квадратные корни из которых извлекаются аналогичным образом и являются целыми? Укажите все такие двузначные числа.2. ABC – равнобедренный треугольник с вершиной А. ?А=27°. Точка D симметрична точке В относительно А. Чему равен угол ?BCD?3. Мальчик стоит на автобусной остановке и мёрзнет, а автобуса нет. Ему хочется пройтись до следующей остановки. Мальчик бегает вчетверо медленнее автобуса и может увидеть автобус на расстоянии 2 км. До следующей остановки ровно километр. Имеет ли смысл идти, или есть риск упустить автобус?Про числа aи b известно, что a = b+ 1. Может ли оказаться так, что a4 = b4?4. Какое наименьшее количество клеток квадрата 5 x 5 нужно закрасить, чтобы в любом квадрате 3 x 3, являющемся его частью, было ровно 4 закрашенных клетки?Олимпиадные задачи по математике 10 класс 1. Постройте эскиз графика функции:. 2. Найдите все значения числового параметра а, при которых корни уравнения положительны.3. Общая хорда двух пересекающихся окружностей служит для одной из них стороной правильного вписанного четырехугольника, а для другой стороной правильного вписанного шестиугольника. Найдите расстояние между центрами окружностей, если радиус меньшей окружности равен 10 см?4. М. В. Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобретал полхлеба и квас. Хватит ли той же денежки ему хотя бы на квас, если цены вырастут еще на 20%? Ответ. Хватит.5. Существует ли выпуклый многоугольник, число диагоналей которого в 10 раз больше числа его сторон? Олимпиадные задачи по математике 11 класс
1. Найдите такое натуральное число k, что 2008! делится на 2007k, но не делится на 2008k. (Напомним, чтоn! = 1·2·3·4·… ·n).2. Может ли вершина параболы y = 4×2 – 4(a + 1)x + a лежать во второй координатной четверти при каком-нибудь значении а?3. (an) – арифметическая прогрессия с разностью 1. Известно, что S2008 — наименьшая среди всех Sn (меньше суммы первых n членов для любого другого значения n). Какие значения может принимать первый член прогрессии?4. Внутри равностороннего треугольника со стороной 8 находится равнобедренный треугольник АВС, в котором АС = ВС = 1, ?С=120°. Две вершины А и В могут лежать либо на одной стороне большого треугольника, либо на двух. Где при этом может оказаться вершина тупого угла – точка С? Нарисуйте это геометрическое место точек и найдите длину соответствующей линии.5. Клетчатая прямоугольная сетка m x n связана из веревочек единичной длины. Двое делают ходы по очереди. За один ход можно разрезать (посередине) не разрезанную ранее единичную веревочку. Если не останется ни одного замкнутого веревочного контура, то игрок, сделавший последний ход, считается проигравшим. Кто из игроков победит при правильной игре и как он должен для этого играть?
Ответы и решения на страницах сайта.
Олимпиады по праву
- Олимпиада СПбГУ для школьников 7–11 классов. Победители могут поступить в Санкт-Петербургский государственный университет без вступительных экзаменов или получить 100 баллов на ЕГЭ по профильному предмету.
- Олимпиада Московской государственной юридической академии имени О.Е. Кутафина для учеников 8-11 классов. Призёры поступают в МГЮА без вступительных экзаменов.
- Межрегиональная олимпиада по праву «Фемида» для учеников 10–11 классов. Победа ученикам 10 класса даёт автоматическое зачисление на очный этап олимпиады в следующем году. Призёры 11 класса зачисляются в Российский государственный университет правосудия без вступительных экзаменов, если наберут 75 баллов на ЕГЭ по обществознанию.
- Московская олимпиада школьников для учащихся 8–11 классов. Призёры 11 класса зачисляются в вуз без вступительных экзаменов. А победители 8–10 классов получают право принимать участие в следующей олимпиаде минуя дистанционный этап.
Олимпиада по математике
Для успешной подготовки к решению олимпиадных заданий, предлагаю попробовать решить реальные варианты задач математических олимпиад. На данном сайте представлены наиболее реалистичные варианты заданий и решение большинства из этих задач. Все варианты заданий взяты с реальных олимпиад. Представлены примеры выполнения заданий, это позволит Вам хорошо подготовиться к олимпиадам и возможно стать даже их призерами, а это уже серьезная заявка на поступление в ВУЗ, так как победители олимпиад имеют льготы при поступлении. Для проверки правильности выполненных заданий, на отдельных страницах приводятся ответы к задачам с вариантами их правильного решения. Удачи.
Задания по математике для 4 класса:
Тест 1 | Тест 2 | Тест 3 | Тест 4 | Тест 5
Олимпиада по математике 5 класс
Олимпиадные задачи по математике 5 класс.Варианты заданий с решением и ответами : 1 вариант | 2 вариант | 3 вариант
Олимпиада по математике 6 класс
Олимпиадные задачи по математике 6 класс.Варианты заданий с решением и ответами : 1 вариант | 2 вариант | 3 вариант
Олимпиада по математике 7 класс
Олимпиадные задачи по математике 7 класс.Варианты заданий с решением и ответами : 1 вариант | 2 вариант | 3 вариант
Олимпиада по математике 8 класс
Олимпиадные задачи по математике 8 класс.Варианты заданий с решением и ответами : 1 вариант | 2 вариант | 3 вариант
Олимпиада по математике 9 класс
Олимпиадные задания по математике 9 класс.Варианты заданий с решением и ответами : 1 вариант | 2 вариант | 3 вариант
Олимпиада по математике 10 класс
Олимпиадные задания по математике 10 класс.Варианты заданий с решением и ответами : 1 вариант | 2 вариант | 3 вариант
Олимпиада по математике 11 класс
Олимпиадные задания по математике 11 класс: Математическая олимпиада физтехаВарианты заданий с решением и ответами : 1 вариант |
2 вариант | 3 вариант
Всероссийская олимпиада по математике | Международная олимпиада по математике
Олимпиадные задания по математике 8 — 11 класс
Новые олимпиадные задания по математике
Олимпиадные задания 8 — 11 класс
Областные олимпиады
Всероссийские олимпиады
Международные олимпиады
Занимательная математика
Занимательная математика : логические задачи, загадки и математические ребусыЗанимательная математика Математические ребусы
Логические задачиЗанимательные задачи по математике
Задачи на смекалку Числовые ребусы
Математические загадки
Интересные задачи по математике Мат-кие загадки на сообразительностьИнтересные математические загадки
Математические загадки в стихах Математические головоломкиМатематическая викторина
Викторина по математике
Великие математики
Основные формулы по математике
Основные формулы по математике
Математика | Геометрия | Тригонометрия | Логарифмы | Сокращенное умножение Производные | Степени | Функции | Англо–американские меры длин, площади и объема
Викторины по математике 1- 8 класс
Математические викторины с ответами, высказывания о математике
Математические викторины для 1 — 8 классов с ответамиВысказывания великих людей о математикеВеликие математики
Всероссийская олимпиада школьников по физике
Во Всероссийской олимпиаде по физике участвуют школьники 7–11 классов. При этом в 7 и 8 классах присутствуют только школьный и муниципальный этапы; для семиклассников и восьмиклассников роль регионального и заключительного этапов играет олимпиада им. Дж. К. Максвелла.
В 9–11 классах Всероссийская олимпиада проводится полноформатно — в четыре этапа.
Муниципальный этап проходит в заранее установленный день. Предлагается четыре-пять задач различной степени сложности.
Региональный и заключительный этапы проходят по единой схеме: теоретический тур и экспериментальный тур. На теоретическом туре даётся пять задач, каждая оценивается в 10 баллов. Экспериментальный тур содержит два задания, каждое по 15 баллов. Таким образом, как на регионе, так и в финале школьник может набрать максимум 80 баллов.
В следующих трёх таблицах можно посмотреть граничные баллы победителей и призёров (соответственно в 9, 10 и 11 классе) последних региональных этапов Всероссийской олимпиады по физике в Москве, а также проходные баллы на заключительный этап.
| РЭ 9 класс | Призёр | Победитель | Проходной |
|---|---|---|---|
| 2019/20 | 26 | 63 | 56 |
| 2018/19 | 40 | 75 | 70 |
| 2017/18 | 25 | 63 | 55 |
| 2016/17 | 30 | 70 | 64 |
| 2015/16 | 34 | 65 | 57 |
| РЭ 10 класс | Призёр | Победитель | Проходной |
|---|---|---|---|
| 2019/20 | 30 | 63 | 58 |
| 2018/19 | 40 | 66 | 62 |
| 2017/18 | 35 | 68 | 63 |
| 2016/17 | 30 | 60 | 53 |
| 2015/16 | 35 | 65 | 57 |
| РЭ 11 класс | Призёр | Победитель | Проходной |
|---|---|---|---|
| 2019/20 | 30 | 60 | 55 |
| 2018/19 | 35 | 66 | 58 |
| 2017/18 | 45 | 69 | 67 |
| 2016/17 | 30 | 60 | 56 |
| 2015/16 | 36 | 70 | 62 |
Хорошо видно, что проходной балл может значительно варьироваться от года к году, поэтому опираться на опыт прошлых лет нет никакого смысла: всё зависит только от того, как написали в этом году остальные участники. Единственный ориентир — проходной обычно на несколько баллов меньше границы победителей в Москве.
В следующей таблице приведены задания Всероссийской олимпиады по физике последних лет, в частности — все варианты предпоследнего и заключительного этапов за всю историю Всероссийской олимпиады (с 1992 года). На пересечении строки (ваш класс) и столбца (этап Всеросса) находятся ссылки на варианты. Цифры ссылки — год проведения финала олимпиады.
Отметим, что до 2009 года Всероссийская олимпиада состояла из пяти этапов: школьный, муниципальный, региональный, предпоследний (который назывался зональным до 2002 года и федеральным окружным в 2002–2008 годах) и заключительный. С целью единообразия предпоследний этап мы всегда называем региональным.
| ШЭ | МЭ | РЭ | ЗЭ | |
|---|---|---|---|---|
| 7 класс |
, , , , , , |
, , , , , |
, | — |
| 8 класс |
, , , , , , |
, , , , , |
, , |
— |
| 9 класс |
, , , , , |
, , , , |
, , , , , , , , , , , , , , , , , , , , , , |
, , , , , , , , , , , , , , , , , , , , , , |
| 10 класс |
, , , , , |
, , , , |
, , , , , , , , , , , , , , , , , , , , , , |
, , , , , , , , , , , , , , , , , , , , , , |
| 11 класс |
, , , , , |
, , , , |
, , , , , , , , , , , , , , , , , , , , , , |
, , , , , , , , , , , , , , , , , , , , , , |
На основе классификации задач 1992–2017 годов составлены программы подготовки к региональному и заключительному этапам:
- 9 класс;
- 10 класс.
Чтобы успешно подготовиться к экспериментальным турам регионального и заключительного этапов, обязательно ознакомьтесь с соответствующими материалами последних лет.
- Экспериментальный тур регионального этапа (с 2002 года).
- Экспериментальный тур заключительного этапа (с 2000 года).
Командные
Олимпиада
Интернет-карусель
Командное онлайн-соревнование
Решая задачи, важно дать много верных ответов подряд
На таких олимпиадах школьники вместе выполняют задания и борются за общий результат. При этом форматы командных соревнований отличаются в зависимости от предмета и фантазии организаторов.
На математических, физических, химических и биологических состязаниях распространены бои, когда одна команда рассказывает решение, а другая его оспаривает
Или карусель, где для победы не обязательно решить много задач, важно дать много верных ответов подряд
Командные олимпиады — это хороший опыт работы в коллективе. Участники учатся вырабатывать общие решения, уважать чужое мнение, грамотно распределять обязанности. Совместная работа и одна на всех цель сплачивает школьников и повышает мотивацию. По накалу борьбы и зрелищности командные олимпиады похожи на спортивные соревнования и поэтому одинаково интересны как самим участникам, так и тем, кто пришел просто посмотреть и поддержать друзей.