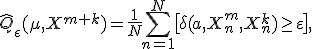Многогранник
Содержание:
- Обобщенная формула Эйлера.
- Геометрические свойстваУглы
- ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
- Виды многоугольников и их свойства
- История
- Платоновы тела.
- Список полуправильных многогранников
- Область применения формулы Эйлера.
- Каталановы тела
- Каталановы тела
- Основные понятия
- Самодвойственные многогранники
- ФОРМУЛА ЭЙЛЕРА
- Важные классы многогранника
- Октаэдр (рис.3).
- Тетраэдр (рис.1).
- Тетраэдр -четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти правильных многоугольников. (рис.1).
- Пирамида
- Параллелоэдры
Обобщенная формула Эйлера.
Для классификации других многогранников используется обобщенная формула Эйлера. Если у некоторого многогранника 16 вершин, 32 ребра и 16 граней, то его эйлерова характеристика равна 16 – 32 + 16 = 0. Это позволяет утверждать, что данный многогранник принадлежит классу многогранников, гомеоморфных тору. Отличительной особенностью этого класса является эйлерова характеристика, равная нулю. Более общо, пусть Р – многогранник с N вершинами, N1 ребрами и N2 гранями. Говорят, что данный многогранник гомеоморфен поверхности рода n в том и только в том случае, если
Наконец, следует заметить, что ситуация существенно усложняется, если смягчить прежнее ограничение, согласно которому никакие две грани многогранника не должны пересекаться. Например, появляется возможность существования двух негомеоморфных многогранников с одной и той же эйлеровой характеристикой. Их следует различать по другим топологическим свойствам.
Геометрические свойстваУглы
С каждым правильным многогранником связаны определённые углы, характеризующие его свойства. Двугранный угол между смежными гранями правильного многогранника {p, q} задаётся формулой:
Иногда удобнее пользоваться выражением через тангенс:
где принимает значения 4, 6, 6, 10 и 10 для тетраэдра, куба, октаэдра, додекаэдра и икосаэдра соответственно.
Угловой дефект при вершине многогранника – это разность между 2π и суммой углов между рёбрами каждой грани при этой вершине. Дефект при любой вершине правильного многогранника:
По теореме Декарта, он равен делённым на число вершин (т.е. суммарный дефект при всех вершинах равен ).
Трёхмерным аналогом плоского угла является телесный угол. Телесный угол Ω при вершине правильного многогранника выражается через двугранный угол между смежными гранями этого многогранника по формуле:
Телесный угол, стягиваемый гранью правильного многогранника, с вершиной в центре этого многогранника, равен телесному углу полной сферы ( стерадиан), делённому на число граней. Он также равен угловому дефекту дуального к данному многогранника.
Различные углы правильных многогранников приведены в следующей таблице. Числовые значения телесных углов даны в стерадианах. Константа – золотое сечение.
| Многогранник | Двугранный уголθ | Плоский угол между рёбрами при вершине | Угловой дефект (δ) | Телесный угол при вершине (Ω) | Телесный угол, стягиваемый гранью | ||
|---|---|---|---|---|---|---|---|
| тетраэдр | 70.53° | 60° | π | π | |||
| куб | 90° | 1 | 90° | ||||
| октаэдр | 109.47° | √2 | 60°, 90° | ||||
| додекаэдр | 116.57° | 108° | |||||
| икосаэдр | 138.19° | 60°, 108° |
Радиусы, площади и объёмы
С каждым правильным многогранником связаны три концентрические сферы:
- Описанная сфера, проходящая через вершины многогранника;
- Срединная сфера, касающаяся каждого его ребра в середине;
- Вписанная сфера, касающаяся каждой его грани в её центре.
Радиусы описанной () и вписанной () сфер задаются формулами:
где θ — двугранный угол между смежными гранями многогранника. Радиус срединной сферы задаётся формулой:
где h — величина описанная выше, при определении двугранных углов (h = 4, 6, 6, 10 или 10). Отношения описанных радиусов к вписанным радиусам симметрично относительно p и q:
Площадь поверхности S правильного многогранника {p, q} вычисляется, как площадь правильного p-угольника, умноженная на число граней Г:
Объём правильного многогранника вычисляется, как умноженный на число граней объём , основанием которой служит правильный p-угольник, а высотой — радиус вписанной сферы r:
Приведённая таблица содержит список различных радиусов, площадей поверхностей и объёмов правильных многогранников. Значение длины ребра a в таблице приравнены к 2.
| Многогранник(a = 2) | Радиус вписанной сферы (r) | Радиус срединной сферы (ρ) | Радиус описанной сферы (R) | Площадь поверхности (S) | Объём (V) |
|---|---|---|---|---|---|
| тетраэдр | |||||
| куб | |||||
| октаэдр | |||||
| додекаэдр | |||||
| икосаэдр |
Константы φ и ξ задаются выражениями
Среди правильных многогранников как додекаэдр, так и икосаэдр представляют собой лучшее приближение к сфере. Икосаэдр имеет наибольшее число граней, наибольший двугранный угол и плотнее всего прижимается к своей вписанной сфере. С другой стороны, додекаэдр имеет наименьший угловой дефект, наибольший телесный угол при вершине и максимально заполняет свою описанную сферу.
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Выпуклый многогранник называется правильным, если он удовлетворяет следующим двум условиям:
-283(i) все его грани – конгруэнтные правильные многоугольники;
(ii) к каждой вершине примыкает одно и то же число граней.
Если все грани – правильные р-угольники и q из них примыкают к каждой вершине, то такой правильный многогранник обозначается {p, q}. Это обозначение было предложено Л.Шлефли (1814–1895), швейцарским математиком, которому принадлежит немало изящных результатов в геометрии и математическом анализе.
Существуют невыпуклые многогранники, у которых грани пересекаются и которые называются «правильными звездчатыми многогранниками». Так как мы условились такие многогранники не рассматривать, то под правильными многогранниками мы будем понимать исключительно выпуклые правильные многогранники.
Виды многоугольников и их свойства
Многоугольник, вписанный в окружность
Многоугольник, описанный около окружности
- Выпуклый многоугольник — это многоугольник, который лежит по одну сторону от любой прямой, содержащей его сторону (то есть продолжения сторон многоугольника не пересекают других его сторон). Существуют и . Выпуклый многоугольник всегда простой, то есть не имеет точек самопересечения.
- Выпуклый многоугольник называется правильным, если у него равны все стороны и все углы, например равносторонний треугольник, квадрат и правильный пятиугольник. Символ Шлефли правильного n{\displaystyle n}-угольника равен {n}{\displaystyle \{n\}}.
- Многоугольник, у которого равны все стороны и все углы, но который имеет самопересечения, называется правильным звёздчатым многоугольником, например, пентаграмма и октаграмма.
- Многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности. Сама окружность при этом называется описанной, а её центр лежит на пересечении серединных перпендикуляров к сторонам многоугольника. Любой треугольник является вписанным в некоторую окружность.
- Многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности. Сама окружность при этом называется вписанной, а её центр лежит на пересечении биссектрис углов многоугольника.. Любой треугольник является описанным около некоторой окружности.
- Выпуклый четырёхугольник называется внеописанным около окружности, если продолжения всех его сторон (но не сами стороны) касаются некоторой окружности. Окружность при этом называется вневписанной. Вневписанная окружность существует также и у произвольного треугольника.
История
Правильные многогранники известны с древнейших времён.
Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона.
В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.
В значительной мере правильные многогранники были изучены древними греками.
Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору.
Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона.
В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
Правильные многогранники характерны для философии Платона, в честь которого и получили название «платоновы тела».
Платон писал о них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику. Земля сопоставлялась кубу, воздух — октаэдру, вода — икосаэдру, а огонь — тетраэдру.
Для возникновения данных ассоциаций были следующие причины: жар огня ощущается чётко и остро (как маленькие тетраэдры);
воздух состоит из октаэдров: его мельчайшие компоненты настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков (к которым ближе всего икосаэдры);
в противоположность воде, совершенно непохожие на шар кубики составляют землю, что служит причиной тому, что земля рассыпается в руках, в противоположность плавному току воды.
По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца».
Аристотель добавил пятый элемент — эфир и постулировал, что небеса сделаны из этого элемента, но он не сопоставлял его платоновскому пятому элементу.
Евклид дал полное математическое описание правильных многогранников в последней, XIII книге Начал.
Предложения 13—17 этой книги описывают структуру тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в данном порядке.
Для каждого многогранника Евклид нашёл отношение диаметра описанной сферы к длине ребра.
В 18-м предложении утверждается, что не существует других правильных многогранников.
Андреас Шпейзер отстаивал точку зрения, что построение пяти правильных многогранников является главной целью дедуктивной системы геометрии в том виде, как та была создана греками и канонизирована в «Началах» Евклида.
Большое количество информации XIII книги «Начал», возможно, взято из трудов Теэтета.
В XVI веке немецкий астроном Иоганн Кеплер пытался найти связь между пятью известными на тот момент планетами Солнечной системы (исключая Землю) и правильными многогранниками.
В книге «Тайна мира», опубликованной в 1596 году, Кеплер изложил свою модель Солнечной системы. В ней пять правильных многогранников помещались один в другой и разделялись серией вписанных и описанных сфер. Каждая из шести сфер соответствовала одной из планет (Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну).
Многогранники были расположены в следующем порядке (от внутреннего к внешнему): октаэдр, за ним икосаэдр, додекаэдр, тетраэдр и, наконец, куб.
Таким образом, структура Солнечной системы и отношения расстояний между планетами определялись правильными многогранниками.
Позже от оригинальной идеи Кеплера пришлось отказаться, но результатом его поисков стало открытие двух законов орбитальной динамики — законов Кеплера, — изменивших курс физики и астрономии, а также правильных звёздчатых многогранников (тел Кеплера — Пуансо).
Платоновы тела.
На рис. 2 изображены правильные многогранники. Простейшим из них является правильный тетраэдр, гранями которого служат четыре равносторонних треугольника и к каждой из вершин примыкают по три грани. Тетраэдру соответствует запись {3, 3}. Это не что иное, как частный случай треугольной пирамиды. Наиболее известен из правильных многогранников куб (иногда называемый правильным гексаэдром) – прямая квадратная призма, все шесть граней которой – квадраты. Так как к каждой вершине примыкают по 3 квадрата, куб обозначается {4, 3}. Если две конгруэнтные квадратные пирамиды с гранями, имеющими форму равносторонних треугольников, совместить основаниями, то получится многогранник, называемый правильным октаэдром. Он ограничен восемью равносторонними треугольниками, к каждой из вершин примыкают по четыре треугольника, и следовательно, ему соответствует запись {3, 4}. Правильный октаэдр можно рассматривать и как частный случай прямой правильной треугольной антипризмы. Рассмотрим теперь прямую правильную пятиугольную антипризму, грани которой имеют форму равносторонних треугольников, и две правильные пятиугольные пирамиды, основания которых конгруэнтны основанию антипризмы, а грани имеют форму равносторонних треугольников. Если эти пирамиды присоединить к антипризме, совместив их основания, то получится еще один правильный многогранник. Двадцать его граней имеют форму равносторонних треугольников, к каждой вершине примыкают по пять граней. Такой многогранник называется правильным икосаэдром и обозначается {3, 5}. Помимо четырех названных выше правильных многогранников, существует еще один – правильный додекаэдр, ограниченный двенадцатью пятиугольными гранями; к каждой его вершине примыкают по три грани, поэтому додекаэдр обозначается как {5, 3}.
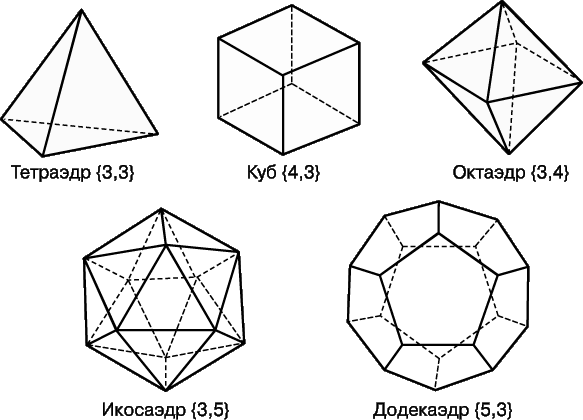
Пять перечисленных выше правильных многогранников, часто называемых также «телами Платона», захватили воображение математиков, мистиков и философов древности более двух тысяч лет назад. Древние греки даже установили мистическое соответствие между тетраэдром, кубом, октаэдром и икосаэдром и четырьмя природными началами – огнем, землей, воздухом и водой. Что касается пятого правильного многогранника, додекаэдра, то они рассматривали его как форму Вселенной. Эти идеи не являются одним лишь достоянием прошлого. И сейчас, спустя два тысячелетия, многих привлекает лежащее в их основе эстетическое начало. О том, что они не утратили свою притягательность и поныне, весьма убедительно свидетельствует картина испанского художника Сальвадора Дали Тайная вечеря.
Древними греками исследовались также и многие геометрические свойства платоновых тел; с плодами их изысканий можно ознакомиться по 13-й книге Начал Евклида. Изучение платоновых тел и связанных с ними фигур продолжается и поныне. И хотя основными мотивами современных исследований служат красота и симметрия, они имеют также и некоторое научное значение, особенно в кристаллографии. Кристаллы поваренной соли, тиоантимонида натрия и хромовых квасцов встречаются в природе в виде куба, тетраэдра и октаэдра соответственно. Икосаэдр и додекаэдр среди кристаллических форм не встречаются, но их можно наблюдать среди форм микроскопических морских организмов, известных под названием радиолярий.
Список полуправильных многогранников
| Многогранник — архимедово тело | Грани | Вершины | Рёбра | Конфигурациявершины | Двойственный — каталаново тело | Группа симметрии |
|---|---|---|---|---|---|---|
|
Кубооктаэдр |
8 треугольников6 квадратов | 12 | 24 | 3,4,3,4 |
Ромбододекаэдр |
Oh |
|
Икосододекаэдр |
20 треугольников12 пятиугольников | 30 | 60 | 3,5,3,5 |
Ромботриаконтаэдр |
Ih |
|
Усечённый тетраэдр |
4 треугольника4 шестиугольника | 12 | 18 | 3,6,6 |
Триакистетраэдр |
Td |
|
Усечённый октаэдр |
6 квадратов8 шестиугольников | 24 | 36 | 4,6,6 |
Тетракисгексаэдр(преломлённый куб) |
Oh |
|
Усечённый икосаэдр |
12 пятиугольников20 шестиугольников | 60 | 90 | 5,6,6 |
Пентакисдодекаэдр |
Ih |
|
Усечённый куб |
8 треугольников6 восьмиугольников | 24 | 36 | 3,8,8 |
Триакисоктаэдр |
Oh |
|
Усечённый додекаэдр |
20 треугольников12 десятиугольников | 60 | 90 | 3,10,10 |
Триакисикосаэдр |
Ih |
|
Ромбокубоктаэдр |
8 треугольников18 квадратов (6 — в кубическом положении, 12 — в ромбическом) | 24 | 48 | 3,4,4,4 |
Дельтоидальный икоситетраэдр |
Oh |
|
Ромбоикосододекаэдр |
20 треугольников30 квадратов12 пятиугольников | 60 | 120 | 3,4,5,4 |
Дельтоидальный гексеконтаэдр |
Ih |
|
Ромбоусечённый кубооктаэдр |
12 квадратов8 шестиугольников6 восьмиугольников | 48 | 72 | 4,6,8 |
Гекзакисоктаэдр |
Oh |
|
Ромбоусечённый икосододекаэдр |
30 квадратов20 шестиугольников12 десятиугольников | 120 | 180 | 4,6,10 |
Гекзакисикосаэдр |
Ih |
|
Курносый куб |
32 треугольника6 квадратов | 24 | 60 | 3,3,3,3,4 | O | |
|
Курносый додекаэдр |
80 треугольников12 пятиугольников | 60 | 150 | 3,3,3,3,5 | I |
Область применения формулы Эйлера.
Значимость формулы Эйлера усиливается тем, что она применима не только к платоновым телам, но и к любому многограннику, гомеоморфному сфере (см. ТОПОЛОГИЯ). Это утверждение доказывается следующим образом.
Пусть P – любой многогранник, гомеоморфный сфере, с N вершинами, N1 ребрами и N2 гранями; пусть c = N – N1 + N2 – эйлерова характеристика многогранника P. Требуется доказать, что c = 2. Так как Р гомеоморфен сфере, мы можем удалить одну грань и превратить остальные в некоторую конфигурацию на плоскости (например, на рис. 5,а и 5,б вы видите призму, у которой удалена передняя плоскость). «Плоскостная конфигурация» представляет собой сеть точек и прямолинейных отрезков, называемых соответственно «вершинами» и «ребрами», при этом вершины служат концами ребер. Вершины и ребра рассматриваемой нами конфигурации мы считаем смещенными и деформированными вершинами и ребрами многогранника. Таким образом, эта конфигурация имеет N вершин и N1 ребер. Остальные N2 – 1 граней многогранника деформируются в N2 – 1 непересекающихся областей на плоскости, определяемой конфигурацией. Назовем эти области «гранями» конфигурации. Вершины, ребра и грани конфигурации и определяют эйлерову характеристику, которая в данном случае равна c – 1.

Теперь мы проведем сплющивание так, что если удаленная грань была р-угольником, то все N2 – 1 граней конфигурации заполнят внутренность р-угольника. Пусть А – некоторая вершина внутри р-угольника. Предположим, что в А сходятся r ребер. Если удалить А и все r сходящихся в ней ребер, то число вершин уменьшится на 1, ребер – на r, граней – на r – 1 (см. рис. 5,б и 5,в). У новой конфигурации Nў0 = N – 1 вершин, Nў1 = N1 – r ребер и Nў2 = N2 – 1 – (r – 1) граней; следовательно,
Таким образом, удаление одной внутренней вершины и сходящихся в ней ребер не меняет эйлеровой характеристики конфигурации. Поэтому, удалив все внутренние вершины и сходящиеся в них ребра, мы тем самым сведем конфигурацию к р-угольнику и его внутренности (рис. 5,г). Но эйлерова характеристика останется по-прежнему равной c – 1, а так как конфигурация имеет р вершин, р ребер и 1 грань, мы получаем
Таким образом, c = 2, что и требовалось доказать.
Далее можно доказать, что если эйлерова характеристика многогранника равна 2, то многогранник гомеоморфен сфере. Иначе говоря, мы можем обобщить полученный выше результат, показав, что многогранник гомеоморфен сфере в том и только в том случае, если его эйлерова характеристика равна 2.
Каталановы тела
Тела, двойственные архимедовым, так называемые каталановы тела, имеют конгруэнтные грани (переводимые друг в друга сдвигом, вращением или отражением), равные двугранные углы и правильные многогранные углы. Каталановы тела тоже иногда называют полуправильными многогранниками. В этом случае полуправильными многогранниками считается совокупность архимедовых и каталановых тел. Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани — правильные многоугольники, но они не одинаковы, а каталановы — в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.
То есть полуправильными в этом случае называются тела, у которых отсутствует только одно из первых двух из следующих свойств правильных тел:
- Все грани являются правильными многоугольниками;
- Все грани одинаковы;
- Тело относится к одному из трёх существующих типов пространственной симметрии.
Архимедовы — тела, у которых отсутствует второе свойство, у каталановых отсутствует первое, третье свойство сохраняется для обоих видов тел.
Существует 13 архимедовых тел, два из которых (курносый куб и плосконосый додекаэдр) не являются зеркально-симметричными и имеют левую и правую формы. Соответственно, существует 13 каталановых тел.
Каталановы тела
Тела, двойственные архимедовым, так называемые каталановы тела, имеют конгруэнтные грани (переводимые друг в друга сдвигом, вращением или отражением), равные двугранные углы и правильные многогранные углы. Каталановы тела тоже иногда называют полуправильными многогранниками. В этом случае полуправильными многогранниками считается совокупность архимедовых и каталановых тел. Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани — правильные многоугольники, но они не одинаковы, а каталановы — в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.
То есть полуправильными в этом случае называются тела, у которых отсутствует только одно из первых двух из следующих свойств правильных тел:
- Все грани являются правильными многоугольниками;
- Все грани одинаковы;
- Тело относится к одному из трёх существующих типов пространственной симметрии.
Архимедовы — тела, у которых отсутствует второе свойство, у каталановых отсутствует первое, третье свойство сохраняется для обоих видов тел.
Существует 13 архимедовых тел, два из которых (курносый куб и плосконосый додекаэдр) не являются зеркально-симметричными и имеют левую и правую формы. Соответственно, существует 13 каталановых тел.
Основные понятия
Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:
- Если вершины являются концами одной стороны, они называются соседними.
- Если отрезок соединяет между собой несоседние вершины, то он имеет название диагонали. У треугольника не может быть диагоналей.
- Внутренний угол — это угол при одной из вершин, который образован двумя его сторонами, сходящимися в этой точке. Он всегда располагается во внутренней области геометрической фигуры. Если многоугольник невыпуклый, его размер может превосходить 180 градусов.
- Внешний угол при определенной вершине — это угол смежный с внутренним при ней же. Иными словами, внешним углом можно считать разность между 180° и величиной внутреннего угла.
- Сумма величин всех отрезков носит название периметра.
- Если все стороны и все углы равны — он носит название правильного. Правильными могут быть только выпуклые.
Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:
- Многоугольник называется плоским, если ограничивает конечную часть плоскости. Эта геометрическая фигура может быть вписанной в окружность или описанной вокруг окружности.
- Выпуклым называется n-угольник, который соответствует одному из условий, приведенных ниже.
- Фигура расположена по одну сторону от прямой линии, которая соединяет две соседних вершины.
- Эта фигура служит общей частью или пересечением нескольких полуплоскостей.
- Диагонали располагаются внутри многоугольника.
- Если концы отрезка располагаются в точках, которые принадлежат многоугольнику, весь отрезок принадлежит ему.
- Фигура может называться правильной, если у нее все отрезки и все углы равны. Примерами могут служить квадрат, равносторонний треугольник или правильный пятиугольник.
- Если n-угольник невыпуклый, все стороны и углы его равны, а вершины совпали с таковыми правильного n-угольника, он называется звездчатым. У таких фигур могут иметься самопересечения. Примерами могут служить пентаграмма или гексаграмма.
- Треугольник или четырехугольник называется вписанным в окружность, когда все его вершины располагаются внутри одной окружности. Если же стороны этой фигуры имеют точки соприкосновения с окружностью, это многоугольник описанным около некоторой окружности.
Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.
Самодвойственные многогранники
Топологически, самодвойственные многогранники — это те многогранники, двойственные которым имеют в точности ту же связь между вершинами, рёбрами и гранями. В абстрактном понимании, это многогранники с идентичными диаграммами Хассе.
Геометрически самодвойственный многогранник является не только топологически самодвойственным, полярное преобразование многогранника относительно некоторой точки, обычно, его центроида, является конгруэнтной фигурой. Например, двойственный многогранник правильного тетраэдра является другим правильным тетраэдром, (центрально симметричным относительно центра тетраэдра).
Любой многоугольник топологически самодвойственен (он имеет то же количество вершин и рёбер, и они меняются местами в результате двойственности), но, в общем случае, не являются геометрически самодвойственными (если рассматривать его как жёсткое тело). Правильные многоугольники геометрически самодвойственны — все углы равны, как и рёбра.
Наиболее принятое геометрическое представление выпуклого многогранника — представление в канонической форме, когда все его рёбра должны касаться некой сферы, центр которой совпадает с центром тяжести точек касания. Если такая фигура самодвойственна, полярное преобразование конгруэнтно ей.
Существует бесконечно много геометрически самодвойственных многогранников. Простейшее бесконечное семейство — пирамиды с n сторонами в канонической форме. Другое бесконечное семейство, , состоит из многогранников, которые можно представить как пирамиды, сидящие на вершинах призм (с тем же числом сторон). Добавьте усечённую пирамиду снизу призмы, и вы получите ещё одно бесконечное семейство.
Существует много других выпуклых самодвойственных многогранников. Например, существует 6 различных многогранников с 7 вершинами и 16 с 8 вершинами
Можно найти также невыпуклые самодвойственные многогранники, такие как
|
3 |
4 |
5 |
6 |
7 |
ФОРМУЛА ЭЙЛЕРА
Рассматривая таблицу, можно заметить интересное соотношение между числом вершин N, числом ребер N1 и числом граней N2 любого выпуклого правильного многогранника {p, q}. Речь идет о соотношении
которое называется формулой Эйлера в честь открывшего ее Л.Эйлера (1707–1783). Левая часть формулы (4) называется «эйлеровой характеристикой».
Формула Эйлера используется в сочетании с формулами (2) и (3). Из (4) и (2) получаем:
Отсюда следует выражение для N1 через p и q:
где
Воспользовавшись еще раз формулой (2), находим аналогичные выражения для N и N2:
Подставляя полученные выражения в формулы (3) и (4), получаем, что число прямых симметрий многогранника {p, q} равно
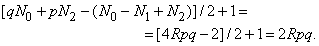
Это число можно записать также в одной из эквивалентных форм: qN, 2N1 или pN2.
Важные классы многогранника
Регулярные многогранники
Регулярный многогранник — наиболее очень симметрический вид с различными группами элементов, являющихся переходным на symmetries многогранника, такого, что многогранник, как говорят, переходный на его флагах. Таким образом двойной из регулярного многогранника также регулярный.
Есть три главных класса регулярного многогранника, которые происходят в любом номере n размеров:
- Simplices, включая равносторонний треугольник и регулярный четырехгранник.
- Гиперкубы или многогранники меры, включая квадрат и куб.
- Orthoplexes или взаимные многогранники, включая квадратный и регулярный октаэдр.
Размеры два, три и четыре включают правильные фигуры, у которых есть пятикратный symmetries и некоторые из которых являются невыпуклыми звездами, и в двух размерах, есть бесконечно много регулярных многоугольников симметрии n-сгиба, и выпуклой и (для n ≥ 5) звезда. Но в более высоких размерах нет никаких других регулярных многогранников.
В трех измерениях выпуклые платонические твердые частицы включают пятикратно-симметричный додекаэдр и икосаэдр, и есть также четыре звезды многогранники Кепле-Пуансо с пятикратной симметрией, принося общее количество к девяти регулярным многогранникам.
В четырех размерах регулярные 4 многогранника включают одно дополнительное выпуклое тело с четырехкратной симметрией и два с пятикратной симметрией. Есть десять звезд 4 многогранника Шлефли-Гесса, все с пятикратной симметрией, давая во всех шестнадцати регулярных 4 многогранниках.
Выпуклые многогранники
Многогранник может быть выпуклым. Выпуклые многогранники — самый простой вид многогранников и формируют основание для нескольких различных обобщений понятия многогранников. Выпуклый многогранник иногда определяется как пересечение ряда полумест. Это определение позволяет многограннику не быть ни ограниченным, ни не конечное. Многогранники определены таким образом, например, в линейном программировании. Многогранник ограничен, если есть шар конечного радиуса, который содержит его. Многогранник, как говорят, указан, если он содержит по крайней мере одну вершину. Каждый ограниченный непустой многогранник указан. Пример нерезкого многогранника — набор. Многогранник конечен, если он определен с точки зрения конечного числа объектов, например, как пересечение конечного числа полусамолетов.
Звездные многогранники
Невыпуклый многогранник может самопересекаться; этот класс многогранников включает звездные многогранники. Некоторые регулярные многогранники — звезды.
Октаэдр (рис.3).
В школе Пифагора было открыто существование несоизмеримых величин, т. е. таких, отношение между которыми невозможно выразить никаким целым или дробным числом. Примером может служить отношение длины диагонали квадрата к длине его стороны, равное Ц2. Число это не является рациональным (т. е. целым или отношением двух целых чисел) и называется иррациональным, т.е. нерациональным (от латинского ratio — отношение).
Тетраэдр
(рис.1).
Тетраэдр
-четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти правильных многоугольников. (рис.1).
Пирамида
-
На рисунке изображены пятиугольная пирамида SABCDE
и ее развертка. Треугольники, имеющие общую вершину, называют боковыми гранями
пирамиды; общую вершину боковых граней — вершиной
пирамиды; многоугольник, которому не принадлежит эта вершина,- основанием
пирамиды; ребра пирамиды, сходящиеся в ее вершине,- боковыми ребрами
пирамиды. Высота
пирамиды — это отрезок перпендикуляра, проведенного через ее вершину к плоскости основания, с концами в вершине и на плоскости основания пирамиды. На рисунке отрезок SO
— высота пирамиды.
Объемы зерновых амбаров и других сооружений в виде кубов, призм и цилиндров египтяне и вавилоняне, китайцы и индийцы вычисляли путем умножения площади основания на высоту. Однако древнему Востоку были известны в основном только отдельные правила, найденные опытным путем, которыми пользовались для нахождения объемов для площадей фигур. В более позднее время, когда геометрия сформировалась как наука, был найден общий подход к вычислению объемов многогранников.
Параллелоэдры
(выпуклые М., найденные Е. С. Фёдоровым, 1881) – М., рассматриваемые как тела, параллельными переносами которых можно заполнить всё бесконечное пространство так, чтобы они не входили друг в друга и не оставляли пустот между собой, т. е. образовать разбиение пространства. Таковы, напр., куб или правильная 6-угольная призма. Существует 5 топологически разл. сеток рёбер параллелоэдров (см. рис. 2, 26–30). Число их граней – 6, 8, 12, 12, 14. Для того чтобы М. был параллелоэдром, необходимо и достаточно, чтобы он был выпуклым М. одного из 5 указанных топологич. типов и чтобы все грани его имели центры симметрии.
Если параллелоэдры разбиения смежны целыми гранями, разбиение называется нормальным. Центры параллелоэдров такого разбиения образуют решётку, т. е. совокупность всех точек с целыми координатами относительно какой-то (вообще говоря, не прямоугольной) декартовой системы координат. Множество точек пространства, из которых каждая отстоит от некоторой данной точки $O$ рассматриваемой решётки Λ не дальше, чем от всякой др. точки этой решётки, называется областью Вороного $D_{OΛ}$ точки $O$ в решётке Λ. Область $D_{OΛ}$ является выпуклым М. с центром в точке $O$. Совокупность областей Вороного всех точек произвольной решётки образует нормальное разбиение пространства. Произвольное (даже $n$-мерное) нормальное разбиение на параллелоэдры, в каждой из вершин которого сходится $n+1$ параллелоэдр, может быть аффинным преобразованием превращено в разбиение Вороного для некоторой решётки.
Всякое движение, переводящее в себя решётку Λ и оставляющее на месте точку $O$, преобразует в себя область $D_{OΛ}$ и обратно. Существует 7 групп таких движений: кубическая, ромбоэдрическая, квадратная (или тетрагональная), ортогональная (или ромбическая), моноклинная, триклинная и гексагональная.