Как подготовиться к дви по математике в мгу

На какие факультеты необходимо сдавать ДВИ по математике в МГУ?

ДВИ необходимо для поступления на технические и математические факультеты, а также ряд специальностей естественно-научных или даже гуманитарных направлений.

Программы очного бакалавриата, на которые необходимо сдавать ДВИ по математике МГУ в 2018 году:

1. Прикладная математика и информатика
2. Математика
3. Механика
4. Фундаментальная информатика и информационные технологии
5. Прикладные математика и физика
6. Химия, физика и механика материалов
7. Геология
8. Биоинженерия и биоинформатика
9. Инноватика
10. Экономика (экономический факультет)
11. Экономика (Высшая школа государственного аудита)
12. Экономика (московская школа экономики)
13. Менеджмент (экономический факультет)
14. Менеджмент (факультет государственного управления)
15. Менеджмент (Высшая школа бизнеса)
16. Менеджмент (социологический факультет)

Как готовиться?

Если выпускник обладает достаточной усидчивостью и целеустремленностью, подготовиться к ДВИ он вполне может самостоятельно. Сегодня в продаже имеется немало пособий с задачами, приблизительно аналогичными тем, что приходится решать во время вступительных испытаний. С заданиями ДВИ за прошлые годы можно познакомиться на сайте мехмата и Центральной приемной комиссии МГУ.

Для подготовки к ДВИ также можно нанять репетитора или пойти на курсы при интересующем вас факультете. Последний вариант может оказаться более предпочтительным, поскольку преподаватели курсов обычно участвуют в разработке заданий для ДВИ и проверке экзаменов, поэтому хорошо представляют, какие навыки и знания необходимы абитуриентам для поступления. В зависимости от факультета и отделения, начинать посещать курсы рекомендуется за год или даже за два до поступления.

Тест № 2

3. О двух треугольниках известно, что длины сторон первого образуют арифметическую прогрессию, а второй является равносторонним. Известно, что их периметры совпадают и равны 3 см, а площади относятся как 4:5. Определить стороны треугольников.

4. Решить неравенство
\
5. Решить неравенство при всех значениях параметра а
\
6. Определить а, если известно, что уравнение
\
имеет четыре различных корня.

7. Решить неравенство
\
8. Решить уравнение
\
9. В выпуклый четырехугольник ABCD с углами \( \angle A = 5\pi/9 \) и \( \angle B = 7\pi/18 \) вписана окружность, касающаяся отрезков АВ, ВС, CD, AD в точках E, F, G, H соответственно. Найти угол FGH.

10. В правильном тетраэдре ABCD с ребром а точка F является серединой ребра CB, а точка E — серединой отрезка DF. Найти такую точку Н на ребре DC, чтобы расстояние АН + НЕ было минимальным. Чему равно это расстояние?

Типы заданий

Для решения задач ДВИ по математике достаточно знаний в рамках школьной программы. Программы ДВИ выложены на сайте центральной приёмной комиссии МГУ. Стоит иметь в виду, что никакого регламента относительно структуры экзамена нет, но за восемь лет проведения ДВИ сложилась некоторая традиция. Каждый из вариантов этих лет содержал по 8 задач. Две первых обычно достаточно простые, следующие две — посложнее, сложнее профильного ЕГЭ, но не намного. Оставшиеся четыре задачи требуют заметно более высоких знаний.

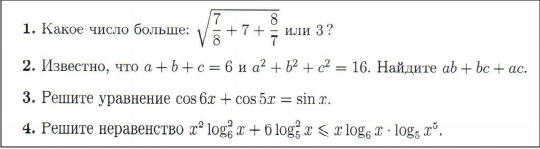
Пример заданий 1—4 из варианта ДВИ 2017 года

Почти всегда в задачах присутствуют логарифмы, показательные функции, корни, модули, тригонометрия — это традиционный набор обычного вступительного экзамена прошлых лет.

Пример задачи по планиметрии из варианта ДВИ 2012 года

Очень часто экзамен включает трудную задачу по планиметрии и часто — по стереометрии. Также часто попадаются текстовые задачи, и почти всегда встречается задача с несколькими переменными или с параметром.

Пример текстовой задачи из варианта ДВИ 2016 года

Общезначимые книги для подготовленных читателей

В. И. Арнольд. Дополнительные главы теории обыкновенных дифференциальных уравнений.

В.И. Арнольд. Лекции об уравнениях с частными производными.

М. Атья. Лекции по K-теории.

Э.Б. Винберг, В.Л. Попов. Теория инвариантов.

Э.Б. Винберг, А.Л. Онищик. Семинар по группам Ли и алгебраическим группам.

С. И. Гельфанд, Ю. И. Манин. Методы гомологической алгебры. Введение в когомологии и производные категории. Том 1

Ф. Гриффитс, Дж. Харрис. Принципы алгебраической геометрии.

М. Громов. Гиперболические группы.

S.K. Donaldson, P.B. Kronheimer. The geometry of 4-manifolds.

Г. Клеменс. Мозаика теории комплексных кривых.

Р. Курант, Д. Гильберт. Методы математической физики.

Ю. И. Манин. Введение в аффинные схемы и квантовые группы.

Дж. Милнор. Теория Морса.

Дж. Милнор. Введение в алгебраическую K-теорию.

Дж. Милнор, Дж. Сташеф. Характеристические классы.

М. Рид, Б. Саймон. Методы современной математической физики.

Ж.-П. Серр. Курс арифметики.

Ж.-П. Серр. Алгебры Ли и группы Ли.

Я.Г. Синай. Введение в эргодическую теорию.

В. Феллер. Теория вероятностей.

Дж. Харрис. Алгебраическая геометрия. Начальный курс.

И. Р. Шафаревич. Основы алгебраической геометрии.

А.Н. Ширяев. Вероятность.

М.А.Шубин. Лекции об уравнениях математической физики.

Критерии оценки ДВИ по математике в МГУ

Максимальная оценка, которую можно получить по ДВИ – 100 баллов. При этом критерии их начисления от года к году разнятся, в зависимости от общего количества поступающих и того, как абитуриенты в целом справились с работой. После проверки всех работ собирается статистика, после чего принимается решение о градации технических баллов за задания экзаменационных работ по 100-балльной шкале.

Обычно 100 баллов можно получить, правильно решив 7 заданий, а в некоторые годы максимальный балл приносило даже решение 6 задач. Для получения минимального положительного балла необходимо набрать 35 баллов (правильно решить одну задачу и показать прогресс в другой). Для большинства технических факультетов, при хорошо сданном ЕГЭ, гарантированное поступление дает результат ДВИ 75–80 баллов. Заметим, что на эту оценку пишут экзамен не более 5 % от общего количества абитуриентов.

В 2017 году соответствие технических баллов и оценок выглядело так:

Общий технический балл	1,5	2	2,5	3	3,5	4	4,5	5	5,5	6	6,5	7 и более
Оценка	36	37	38	40	45	55	60	70	75	85	90	100

ДВИ по математике в МГУ сдается в письменном виде

Программа подготовки абитуриентов к экзамену

• Натуральные числа. Целые числа. Делимость натуральных чисел. Признаки делимости натуральных чисел на 2, 3, 4, 5, 9, 10. Простые и составные числа. Наибольший общий делитель. Наименьшее общее кратное.
• Рациональные числа. Арифметические действия над рациональными числами. Основное свойство дроби.
• Отношения и пропорции.
• Проценты.
• Бесконечные десятичные дроби. Периодические десятичные дроби.
• Иррациональные числа. Множество действительных чисел. Числовая ось.
• Модуль действительного числа, его свойства.

• Степень с натуральным показателем.
• Степень с целым показателем.
• Рациональные выражения. Тождественные преобразования. Тождества.
• Одночлены. Многочлены. Действия над одночленами и многочленами.
• Формулы сокращённого умножения. Разложение многочлена на множители. Деление многочленов.
• Корень n-й степени из действительного числа. Арифметический корень n-й степени. Правила действий над корнями.
• Степень с рациональным и действительным показателем.
• Логарифмы. Свойства логарифмов.

• Уравнения и его корни. Равносильные уравнения.
• Линейные уравнения с одной переменной. Системы линейных уравнений.
• Уравнения, содержащие переменную в знаменателе дроби.
• Квадратные уравнения.
• Иррациональные уравнения.
• Показательные уравнения.
• Логарифмические уравнения.
• Уравнения, содержащие переменную под знаком модуля.
• Уравнения с параметром.
• Графический метод решения уравнения.

• Основные свойства числовых неравенств.
• Неравенства с одной переменной.
• Линейные неравенства с одной переменной. Системы линейных неравенств.
• Двойные неравенства.
• Неравенства второй степени с одной переменной.
• Неравенства, содержащие переменную под знаком модуля.
• Дробно-рациональные неравенства и системы неравенств.
• Иррациональные неравенства и системы неравенств.
• Показательные неравенства.
• Логарифмические неравенства.
• Неравенства, содержащие параметр.

• Числовая последовательность.
• Арифметическая прогрессия.
• Геометрическая прогрессия. Бесконечно убывающая геометрическая прогрессия.

• Радианное измерение углов и дуг. Соотношения между градусной и радианной мерами углов.
• Тригонометрические функции числового аргумента.
• Периодичность тригонометрических функций.
• Соотношения между тригонометрическими функциями одного аргумента.
• Тригонометрические функции суммы и разности двух углов.
• Тригонометрические функции двойного и половинного угла.
• Выражение тригонометрических функций через тангенс половинного угла.
• Формулы суммы и разности тригонометрических функций.
• Преобразование произведений тригонометрических функций в полу-сумму и полуразность.
• Формулы понижения степени.
• Непрерывность тригонометрических функций.
• Производные тригонометрических функций.
• Свойства и графики функций: у = sin x, y = cos x, y = tg x, y = ctg x.
• Обратные тригонометрические функции.
• Тригонометрические уравнения и системы.
• Тригонометрические неравенства.

• Понятие функции. Область определения функции. Область значений функции. Чётные и нечётные функции. Монотонные функции. Периодические функции.
• Степенная функция.
• Показательная функция.
• Обратная функция.
• Логарифмическая функция.
• Алгебраические функции.
• Преобразования графиков функций.

• Производная, её геометрический и физический смысл.
• Основные правила дифференцирования.
• Производная сложной функции.
• Основные формулы дифференцирования.
• Признаки постоянства, возрастания и убывания функции. Экстремум функции. Необходимое условие экстремума. Достаточное условие экстремума.
• Исследование функций и построение графиков.
• Первообразная функции и способы её нахождения.

• Применение тригонометрии для решения задач планиметрии.
• Метрические соотношения в треугольнике.
• Окружность. Центральные углы, вписанные углы.
• Вписанные и описанные многоугольники.
• Периметр и площади треугольников и четырёхугольников.

• Многогранники. Призма. Параллелепипед. Пирамида. Правильные многогранники.
• Тела вращения. Цилиндр. Конус. Шар.
• Объёмы тел и площади поверхностей.

• Сведение текстовой задачи к уравнению или системе уравнений.
• Задачи на доли и части.
• Задачи на движение.
• Задачи на работу.

Системы линейных уравнений

Пример 9. Метод Крамера

Дано:
Система линейных уравнений

Найти:
Решение системы линейных уравнений методом Крамера.x₁, x₂, x₃— ?

Составляем матрицу B из свободных членов данной системы уравнений — матрицу-столбец свободных членов:

Решаем пример методом Крамера, используя .

Условие Δ ≠ 0 выполняется, значит система совместна и определена, причём единственное решение вычисляется по формулам Крамера:

Δ₁ — 1-й вспомогательный определитель системы, получается из Δ заменой 1-го столбца на столбец свободных членов:

Δ₂ — 2-й вспомогательный определитель системы, получается из Δ заменой 2-го столбца на столбец свободных членов:

Δ₃ — 3-й вспомогательный определитель системы, получается из Δ заменой 3-го столбца на столбец свободных членов:

Подставив полученные значения в формулы Крамера, находим неизвестные члены уравнения: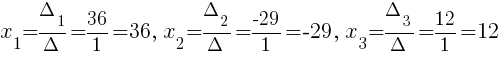

Ответ: .

Пример 10. Метод Гаусса

Дано:
Система линейных уравнений

Найти:
Решение системы линейных уравнений методом Гаусса.x₁, x₂, x₃— ?

Решение:
Составляем расширенную матрицу (A|B) системы из коэффициентов при неизвестных и правых частей:
(A|B)=

Приведём расширенную матрицу (A|B) системы к ступенчатому виду.

Из второй строки вычитаем первую строку, умноженную на четыре:
(A|B)~

Из третьей строки вычитаем первую строку, умноженную на два:
(A|B)~

Из третьей строки вычитаем вторую строку, умноженную на :
(A|B)~

Полученной диагональной матрице соответствует эквивалентная система: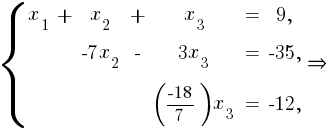

Ответ: .

Первое, и самое ценное

В условиях дефицита «вменяемой» учебной литературы важнейшим источником информации становятся ваши собственные записи лекций. Ваши. Собственноручные. Когда я рассказывал о системности очного образования, то советовал посещать максимальное количество лекций, и сейчас немного остановлюсь на технической стороне вопроса. Старайтесь оформлять свои конспекты как можно качественнее – как минимум, разборчиво и достаточно пОлно. В течение ближайших дней записи полезно перечитать, при этом не нужно ставить перед собой идеалистической цели «во всём разобраться и всё запомнить». Если вы хоть что-то дополнительно поняли, если вспомнили и пометили какие-то важные моменты, если осознали второстепенные, то это уже хороший результат, даже отличный 😉

Это, кстати, касается не только «технических», но и гуманитарных предметов. С тем отличием, что там проблема противоположная – можно утонуть в море информации, и то, что «размазано» по 100 страницам 10 учебников, порой, умещается на один лист конспекта. Вы знаете, где философия Гегеля занимает половину печатной страницы? Вы видели много таких книг? Я встретил только одну: сталинский философский словарь. Всё коротко, всё чётко, ВСЁ ПОНЯТНО, и, главное, ничего не смешано с пропагандой: сначала излагается суть философии, её тезисы, и только затем обосновывается, что она «ложна и антинаучна».

И как ни странно, первое, на что нужно обратить внимание при выборе литературы – это год выпуска. Если учебник издан в 70-х годах XX века и ранее, то к нему уже стОит присмотреться

Это лучшие традиции советской педагогической школы, которые выдержаны, в частности, в упомянутом выше словаре. Далее педагогика начала деградировать – учебники (не все, конечно), в том числе школьные, стали становиться всё более «водяными» и наукообразными, и всё менее и менее понятными.

Со школьной литературы и начнём, среди моих читателей немало учащихся старших классов, да и школьный материал ведь многие позабыли.

Поехали:

1) Если у вас пробелы или проблемы в понимании элементарной математики, то однозначно рекомендую учебники А. П. Киселёва, тут без комментариев – это целая эпоха и можно сказать легенда отечественного математического образования. Кроме того, (как по мне) неплох учебник по геометрии Л.С. Атанасяна, который выдержал более 20 переизданий; я сам учился по этому учебнику, и он оставил хорошие впечатления

3) Краснов М. Л., Киселев А. И., Макаренко Г. И. и др. Решебники по различным разделам высшей математики. Лично пользовался «Дифференциальными уравнениями» и «Функциями комплексного переменного», и признаЮ, что содержание действительно соответствует заявленной миссии: в книгах кратко излагается теория и достаточно подробно объясняются решения. Однако начинающим будет понятно далеко не всё, и я напоминаю, что у вас есть я 🙂  

4) Атанасян Л. С., Базылев В. Т. Геометрия в 2 томах – Учебник для педагогических вузов. По роду своей профессиональной подготовки мне известен именно этот учебник, в частности, чтобы освоить аналитическую геометрию – хватит «за глаза и за уши». Хотя наверняка существуют и другие, более простые учебники, пишите, если вам таковые известны!

5) Математический анализ. Мой любимый раздел высшей математики, по которому могу посоветовать сразу несколько источников.

Попроще:

Бохан К. А. Курс математического анализа, 2 тома – учебник для заочников педагогических вузов;

Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, 2 тома.

Посложнее:

Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, 3 тома – развёрнутый курс с многочисленными примерами и типично «матановской» лексикой.

Посолиднее:

Ильин В. А., Садовничий В. А. Математический анализ, 2 тома, издательство МГУ – более обстоятельный источник с научным стилем изложения, в котором рассматриваются моменты, умалчиваемые в других книгах.

Выбирайте по уровню подготовки и потребностям!

Составьте свой календарь абитуриента

Чтобы не запутаться в сроках и датах, не опоздать со сдачей документов, составьте для себя календарь абитуриента на 2018 год. Отметьте в нем все самые важные даты. Начните с основных:

• 20 июня – начало приема документов;
• 26 июля – завершение приема документов, окончание вступительных испытаний;
• 27 июля – размещение списка поступающих на сайте вуза или стенде приемной комиссии;
• 28 июля – последний день приема заявлений о согласии на зачисление.

Не забудьте отметить сроки начала и конца сдачи дополнительных вступительных испытаний в вашем вузе, если они есть. Информацию о них и других важных для вашей специальности мероприятиях вы можете узнать на сайте вуза или в личном кабинете поступающего (если прошли регистрацию на сайте учебного заведения).

Если требуется прохождение медицинской комиссии, сделать это можно в любой государственной поликлинике или лицензированном частном центре. Справка действительна в течение 6 месяцев.

Не забудьте о том, что вуз может начислить вам баллы за индивидуальные достижения.

Уточняйте всю дополнительную информацию о поступлении в приемной комиссии

Глава 6. Классификация грамматических ошибок

Упражнение № 4

Проблема различения понятий «патриотизм» и «национализм» волнует автора.

Довольно часто одно понятие подменяется другим. Но если патриотизм выражает силу нации, то национализм – её ограниченность и слабость. Шокируют порой газетные материалы, рассказывающие о межнациональных конфликтах.

В дополнение хочется сказать, что отношения людей любой расы и национальности должны строиться на взаимоуважении. 

Упражнение № 5

Смешение лексики разных стилей.

1) В деревенском очаге культуры был настоящий дубак.

2) Наташа Ростова любила одного парня, а руку и сердце хотела отдать другому.

3) Любой человек может попасть в трудную жизненную ситуацию, и нечего корчить из себя неуязвимого.

Употребление канцеляризмов.

1) Иногда бывает так: человек сам много читает и знает, но не проводит среди населения разъяснительную работу.

2) Автор доводит до сведения читателей свои мысли по этому поводу.

3) В водной среде водились щуки, караси, а также мелкие пескари.

Речевые штампы.

1) Образ Андрея Болконского – типичный пример для подражания.

Функции и графики

Две справочно-прикладные статьи, без которых никуда! Причём во всей вышке:

Графики и свойства элементарных функцийПостроение графиков путём их элементарного преобразования

Основной же цикл статей посвящён исследованию функции:

Непрерывность функцииОбласть определения функцииАсимптоты графика функцииНули и интервалы знакопостоянства функцииВозрастание, убывание и экстремумы функцииВыпуклость, вогнутость и перегибы графикаПолное исследование функции

По материалам перечисленных уроков создан удобный справочный конспект:Схема исследования функции

+ Нахождение наибольшего и наименьшего значений функции на отрезке (самостоятельная задача и иногда «довесок» к полному исследованию)

И бонус:

Главное меню

• • Регистрация на сайте

  • • Сотрудники отдела организации приема абитуриентов
    • Часто задаваемые вопросы
    • Нормативные документы приемной комиссии КФУ
    • Документы об утверждении стоимости обучения
    • Контакты
  • • Мероприятия и события
    • Новости приемной комиссии
    • Буклет

• • Регистрация на сайте

  • • Информирование о приеме
    • Правила приема
    • Калькулятор ЕГЭ
    • План приема (количество мест, вступительные испытания и минимальные баллы)
    • Сроки проведения приема
    • Схема поступления
    • Буклет
    • Справочник для поступающих
    • Медицинский осмотр
    • График проведения Дней открытых дверей 2019-2020
    • Образовательные кредиты
  • • Подача документов
    • Расписание вступительных испытаний
    • Дистанционные вступительные испытания
    • Программа вступительных испытаний
    • Прием в пределах особой квоты (льготники)
    • Прием лиц с ограниченными возможностями здоровья
    • Прием победителей и призеров олимпиад
    • Стипендия ректора «Стобалльник»
    • Преимущественное право зачисления
    • Учет индивидуальных достижений
    • Прием на целевые места
    • Стоимость обучения
    • Общежития
  • • Списки поступающих
    • Приказы о зачислении
    • Поданные заявления о приеме
    • Итоги приема. Архив

• • Регистрация на сайте

  • • Информирование о приеме
    • Правила приема
    • План приема (количество мест, вступительные испытания и минимальные баллы)
    • Сроки проведения приема
    • График проведения Дней открытых дверей
    • Олимпиада для поступающих в магистратуру «Я – Магистрант КФУ»
    • Олимпиада федеральных университетов для поступающих в магистратуру в 2020 г.
    • Образовательные кредиты
  • • Подача документов
    • Расписание вступительных испытаний
    • Дистанционные вступительные испытания
    • Программа вступительных испытаний
    • Прием лиц с ограниченными возможностями здоровья
    • Учет индивидуальных достижений
    • Прием на целевые места
    • Стоимость обучения
    • Медицинский осмотр
    • Общежития
  • • Списки поступающих
    • Приказы о зачислении
    • Поданные заявления о приеме
    • Итоги приема. Архив

• • Регистрация на сайте

  • • План приема
    • Направления обучения
    • Стоимость обучения
    • Образовательные кредиты
  • • Правила приема
    • Инструкция по поступлению
    • Перечень вступительных испытаний
    • Программа вступительных экзаменов
    • Расписание вступительных экзаменов
  • • Списки рекомендованных в аспирантуру
    • Списки поступающих
    • Правила подачи и рассмотрения апелляций по результатам вступительных испытаний
    • Приказы о зачислении

• • Регистрация на сайте

  • • Приемная комиссия по программам ординатуры
    • Правила приема
    • Сроки проведения приема
    • План приема 2020
    • Образовательные кредиты
  • • Подача документов
    • Расписание вступительных испытаний
    • Программа вступительных испытаний
    • Стоимость обучения
    • Образец договора на оказание платных образовательных услуг
    • Общежития
  • • Поданные заявления
    • Списки поступающих
    • Правила подачи и рассмотрения апелляций по результатам вступительных испытаний
    • Результаты вступительных испытаний
    • Приказы о зачислении

• • Регистрация на сайте

  • • Правила приема
    • Документы для поступления
    • Часто задаваемые вопросы
    • Контакты
  • • Правила приема
    • Документы для поступления
    • Часто задаваемые вопросы
    • Контакты
  • • Приказы о зачислении
    • Правила приема
    • Документы для поступления
    • Часто задаваемые вопросы
    • Контакты
• • • Расписание онлайн Дней открытых дверей
    • Прием на обучение по контракту
    • Прием на общих основаниях
    • Прием по квоте
    • Прием соотечественников
    • Требования к документам об образовании абитуриентов
    • Информация для прибытия
    • Правила пребывания иностранных граждан на территории РФ
    • Олимпиады
    • Контакты
  • Бакалавриат / Специалитет
    • Инструкция по поступлению
    • Направления обучения
    • Расписание вступительных испытаний
    • Минимальные баллы для поступления
    • Документы для поступления
  • Магистратура
    • Инструкция по поступлению
    • Направления обучения
    • Расписание вступительных испытаний
    • Минимальные баллы для поступления
    • Документы для поступления
  • • Аспирантура
    • Ординатура
    • Предвузовская подготовка для иностранных граждан и лиц без гражданства
    • Программы обмена
    • Летние школы
    • Зимние школы
    • Дополнительные образовательные программы
• • • Общая информация
    • Факультеты
    • Информация для поступающих
    • Информация для обучающихся
  • • Общая информация
    • Курсы
    • Информация для поступающих
    • Информация для обучающихся
  • • Курсы подготовки к ЕГЭ и ОГЭ
    • Летние подготовительные курсы
    • Пробные экзамены
    • Дистанционные подготовительные курсы
    • Учебные пособия
  • • Межрегиональные предметные олимпиады КФУ
    • Научная конференция им. Н. И. Лобачевского
    • Конкурсы, олимпиады, профильные школы